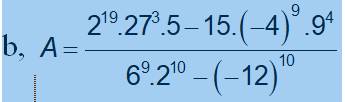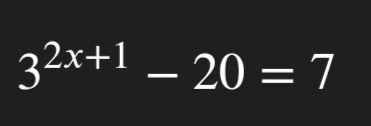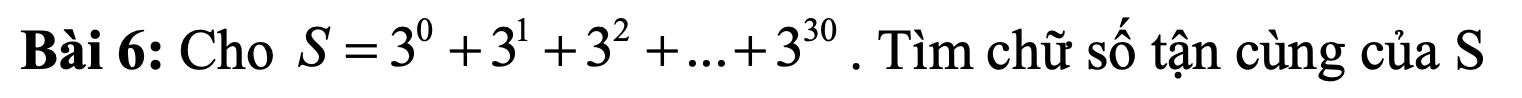NL
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AL
5
NN
2
9 tháng 8 2023
\(=\dfrac{2^{19}\cdot3^9\cdot5+2^{18}\cdot3^9\cdot5}{2^{19}\cdot3^9-2^{20}\cdot3^{10}}\)
\(=\dfrac{2^{18}\cdot3^9\cdot5\left(2+1\right)}{2^{19}\cdot3^9\left(1-2\cdot3\right)}=\dfrac{1}{2}\cdot\dfrac{5\cdot3}{-5}=-\dfrac{3}{2}\)
H9
HT.Phong (9A5)
CTVHS
9 tháng 8 2023
\(A=\dfrac{2^{19}\cdot27^3\cdot5-15\cdot\left(-4\right)^9\cdot9^4}{6^9\cdot2^{10}-\left(-12\right)^{10}}\)
\(A=\dfrac{2^{19}\cdot\left(3^3\right)^3\cdot5-3\cdot5\cdot-\left(2^2\right)^9\cdot\left(3^2\right)^4}{2^9\cdot3^9\cdot2^{10}-\left(2^2\right)^{10}\cdot3^{10}}\)
\(A=\dfrac{2^{19}\cdot3^9\cdot5+3^9\cdot2^{18}\cdot5}{2^{19}\cdot3^9-2^{20}\cdot3^{10}}\)
\(A=\dfrac{2^{18}\cdot3^9\cdot5\cdot\left(2+1\right)}{2^{19}\cdot3^9\cdot\left(1-2\cdot3\right)}\)
\(A=\dfrac{1\cdot1\cdot5\cdot3}{2\cdot1\cdot-5}\)
\(A=-\dfrac{1}{2}\cdot3\)
\(A=-\dfrac{3}{2}\)
H9
HT.Phong (9A5)
CTVHS
8 tháng 10 2023
Dạng 3:
Bài 1:
a) Số lượng số hạng là:
\(\left(999-1\right):1+1=999\) (số hạng)
Tổng dãy là:
\(A=\left(999+1\right)\cdot999:2=499500\)
b) Số lượng số hạng là:
\(\left(100-7\right):3+1=32\) (số hạng)
Tổng dãy là:
\(S=\left(100+7\right)\cdot32:2=1712\)
AH
Akai Haruma
Giáo viên
12 tháng 1 2022
Lời giải:
a. Mẹ An mua thực phẩm hết số tiền là:
$3\times 120000+4\times 50000+20\times 3500+220000=850000$ (đồng)
b. Mẹ An mua thực phẩm và khẩu trang hết:
$850000+2\times 35000=920000$ (đồng)
T
1
KV
28 tháng 10 2023
3²ˣ⁺¹ - 20 = 7
3²ˣ⁺¹ = 7 + 20
3²ˣ⁺¹ = 27
3²ˣ⁺¹ = 3³
2x + 1 = 3
2x = 3 - 1
2x = 2
x = 2 : 2
x = 1
KM
4
DA
1
19 tháng 8 2021
\(2S=3^{31}-1=3^{28}.3^3-1=\left(...1\right).27-1=\left(.....7\right)-1=\left(...6\right)\)
\(\Rightarrow S=\left(...3\right)\)
Tận cùng bằng 3 nhé e
19 tháng 8 2021
3^0 có tận cùng là 1.
3^1 có tận cùng là 3.
3^2 có tận cùng là 9.
3^3 có tận cùng là 7.
3^4 có tận cùng là 1.
................................
3S = ( 3^1+3^2+3^3+......+3^31 )
3S-S = ( 3^1+3^2+3^3+......+3^31 ) - ( 3^0+3^1+3^2+......+3^30 )
2S = 2^31-1
2^31 có tận cùng là 1. ( theo như công thức đã nêu trên )
=> 2S có tận cùng là 0.
2S-S = 2S : 2
=> S có tận cùng là 5 vì ....0 : 2 bằng 5.