
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phân tích đa thức thành nhân tử ?
\(x^3y^6+1=\left(xy^2\right)^3+1=\left(xy^2+1\right)\left(x^2y^4-xy^2+1\right)\)

a) 2 - 3x = x + 5
⇔ -3x - x = -2 + 5
⇔ -4x = 3
⇔ x = -0,75
Vậy PT có tập nghiệm S = { -0,75 }
b) \(2x^2-x-3\left(2x-1\right)=0\)
⇔ \(x\left(2x-1\right)-3\left(2x-1\right)\) = 0
⇒ ( x - 3 ) ( 2x -1 ) = 0
⇔ x - 3 = 0 hoặc 2x - 1 = 0
⇔ x = 3 hoặc x = 0,5
Vậy PT có tập nghiệm S = { 3 ; 0,5 }
c) \(\dfrac{3}{5x-1}+\dfrac{2}{3x-5}=\dfrac{4}{\left(5x-1\right)\left(3x-5\right)}\) ( ĐKXĐ : x ≠ 0,2 và x ≠ \(\dfrac{5}{3}\))
⇔ 3(3x-5) + 2(5x-1) = 4
⇔ 9x - 15 + 10x - 2 = 4
⇔ 19x - 17 = 4
⇔ 19x = 17 + 4
⇔ 19x = 21
⇔ x = \(\dfrac{21}{19}\) ( thỏa mãn ĐKXĐ )
Vậy PT có tập nghiệm S = { \(\dfrac{21}{19}\) }

f: \(3ab-6a+b-2\)
\(=3a\left(b-2\right)+\left(b-2\right)\)
\(=\left(b-2\right)\left(3a+1\right)\)

ĐKXĐ:\(x\ne-2\)
\(\dfrac{1}{x+2}-1=\dfrac{5x+7}{x+2}\\ \Leftrightarrow\dfrac{1}{x+2}-\dfrac{5x+7}{x+2}=1\\ \Leftrightarrow\dfrac{1-5x-7}{x+2}=1\\ \Leftrightarrow-5x-6=x+2\\ \Leftrightarrow x+2+5x+6=0\\ \Leftrightarrow6x+8=0\\ \Leftrightarrow x=-\dfrac{4}{3}\left(tm\right)\)

\(9x^2-1+\left(3x-1\right).\left(x+2\right)=0\)
\(\Leftrightarrow9x^2-1+3x^2+6x-x-2=0\)
\(\Leftrightarrow9x^2+3x^2+6x-x=0+1+2\)
\(\Leftrightarrow12x^2+5x=3\)
\(\Leftrightarrow12x^2+5x-3=0\)
\(\Leftrightarrow12x^2-4x+9x-3=0\)
\(\Leftrightarrow4x\left(3x-1\right)+3\left(3x-1\right)\)
\(\Leftrightarrow\left(4x+3\right)\left(3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+3=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=-3\\3x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3}{4}\\x=\dfrac{1}{3}\end{matrix}\right.\)
Vậy tập nghiệm phương trình là S = \(\left\{\dfrac{-3}{4};\dfrac{1}{3}\right\}\)
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ

a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)

E = 2x2 + 3x + 8
= 2( x2 + 3/2x + 9/16 ) + 55/8
= 2( x + 3/4 )2 + 55/8 ≥ 55/8 ∀ x
Dấu "=" xảy ra khi x = -3/4
=> MinE = 55/8 <=> x = -3/4



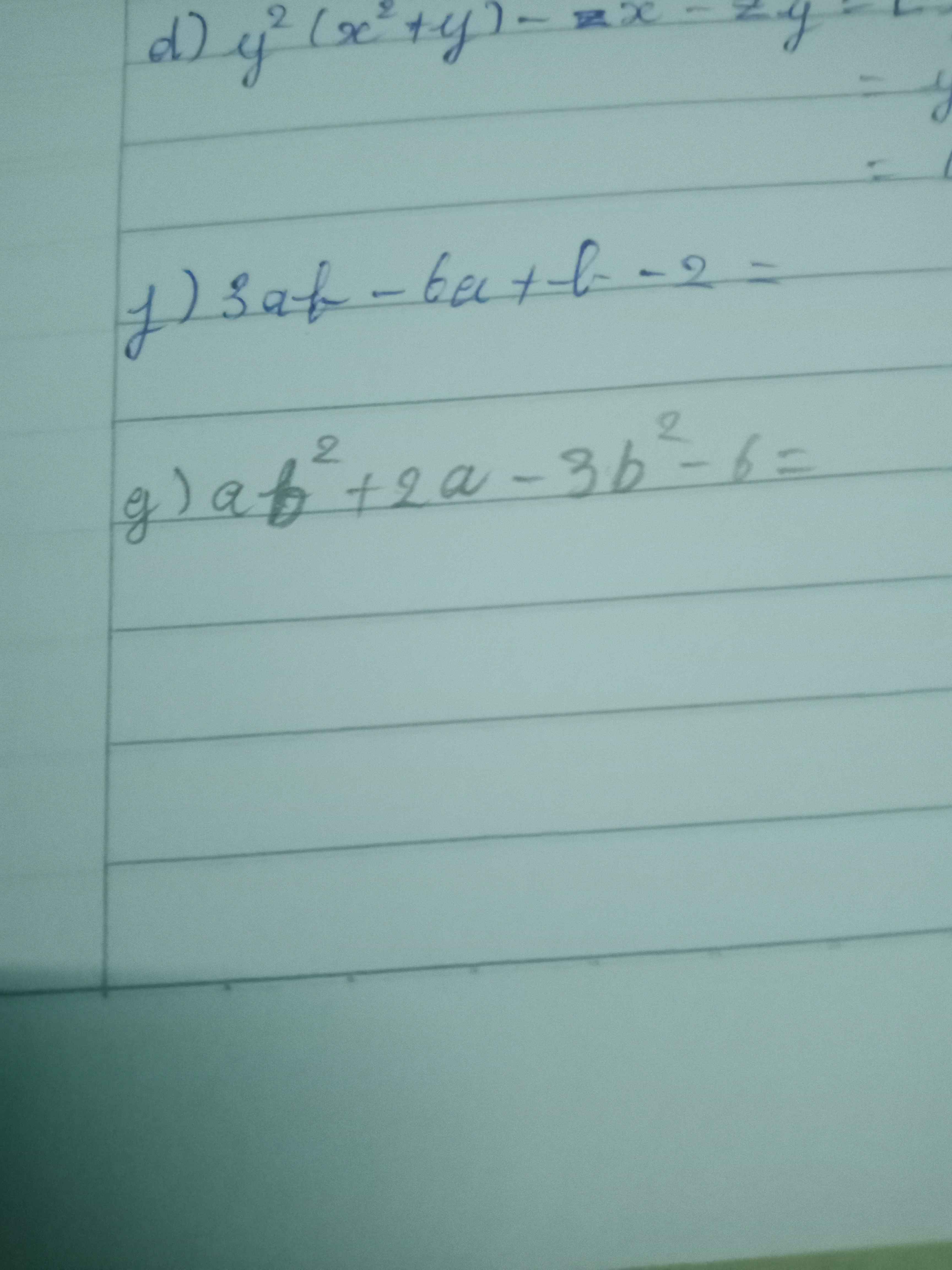
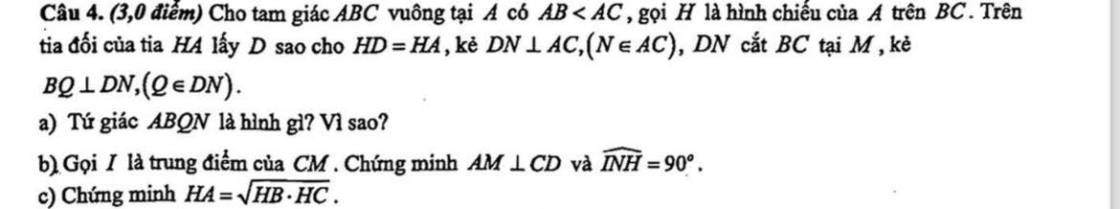

where?