
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a) \(2\left(x+3\right)=4x-\left(2+x\right)\)
\(2x+6=3x-2\)
\(-x=-8\)=>x=8
b) \(\dfrac{1}{x+2}+\dfrac{5}{2-x}=\dfrac{2x-3}{x^2-4}\) đk x khác 2 và -2
\(\dfrac{\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{5\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x-3}{\left(x-2\right)\left(x+2\right)}\)
=>\(x-2-5x-10=2x-3\)
\(-6x=9=>x=\dfrac{3}{2}tm\)

Câu 3:
a: Ta có: \(2x\left(3x-1\right)-\left(x-3\right)\left(6x+2\right)\)
\(=6x^2-2x-6x^2-2x+18x+6\)
=14x+6
b: Ta có: \(2x\left(x+7\right)-3x\left(x+1\right)\)
\(=2x^2+14x-3x^2-3x\)
\(=-x^2+11x\)
Câu 2:
a: Ta có: \(\left(-8x^5+12x^3-16x^2\right):4x^2\)
\(=-8x^5:4x^2+12x^3:4x^2-16x^2:4x^2\)
\(=-2x^3+3x-4\)
b: Ta có: \(\left(12x^3y^3-18x^2y+9xy^2\right):6xy\)
\(=12x^3y^3:6xy-18x^2y:6xy+9xy^2:6xy\)
\(=2x^2y^2-3x+\dfrac{3}{2}y\)
c: Ta có: \(\dfrac{x^3-11x^2+27x-9}{x-3}\)
\(=\dfrac{x^3-3x^2-8x^2+24x+3x-9}{x-3}\)
\(=x^2-8x+3\)
d: Ta có: \(\dfrac{6x^4-13x^3+7x^2-x-5}{3x+1}\)
\(=\dfrac{6x^4+2x^3-15x^3-5x^2+12x^2+4x-5x-\dfrac{5}{3}-\dfrac{10}{3}}{3x+1}\)
\(=2x^3-5x^2+4x-\dfrac{5}{3}-\dfrac{\dfrac{10}{3}}{3x+1}\)

a: Xét tứ giác ANME có
\(\widehat{ANM}=\widehat{AEM}=\widehat{EAN}=90^0\)
Do đó: ANME là hình chữ nhật

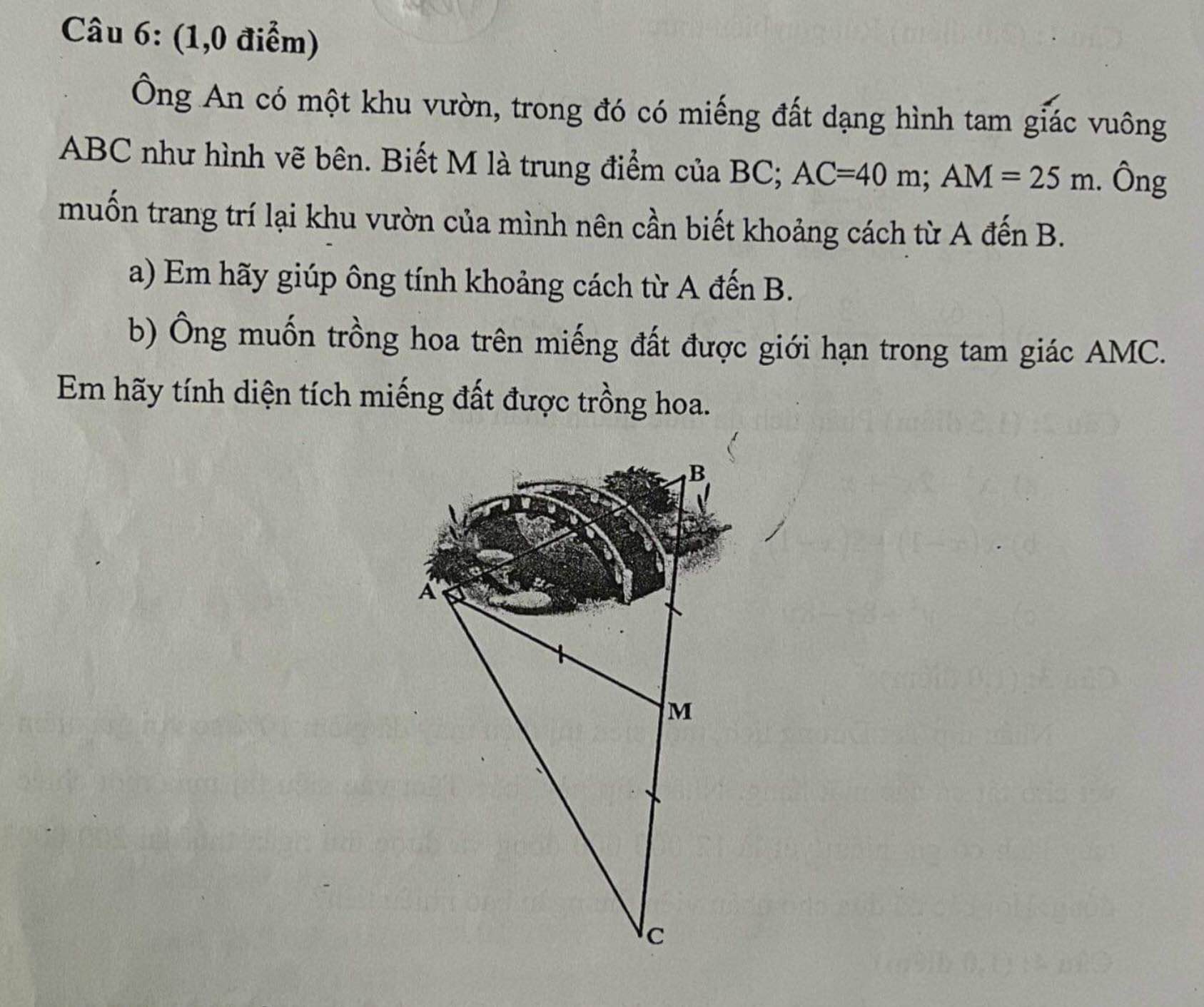
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)

Bài 2:
f: \(x^2+1=\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{x^2-1}=\dfrac{x^4-1}{x^2-1}\)
\(\dfrac{x^4}{x^2-1}=\dfrac{x^4}{x^2-1}\)




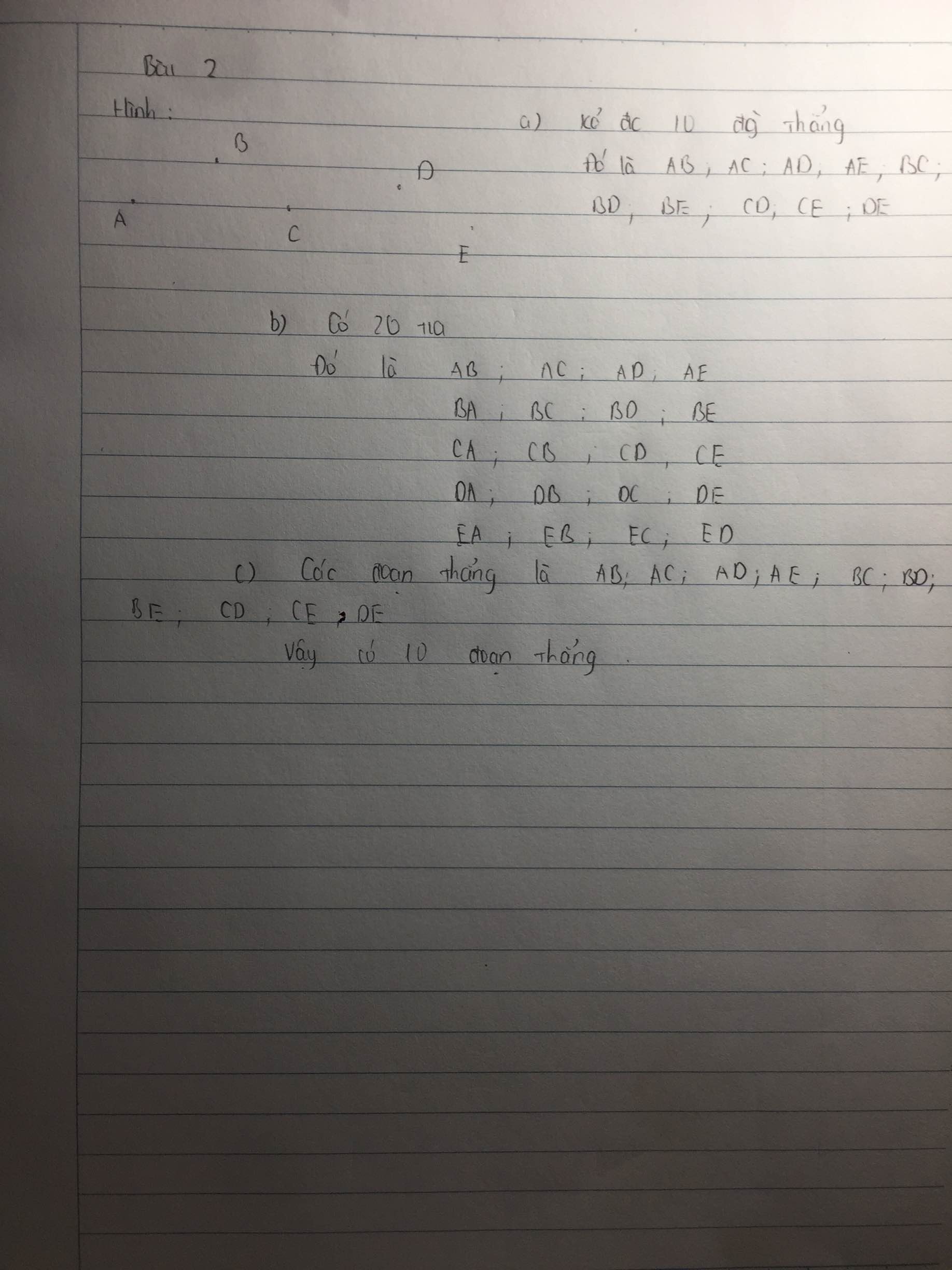
 Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều


 GIÚP EM VS Ạ.CẢM ƠN MNG NHIỀU🥺🥺🥺❤️😘😘😘
GIÚP EM VS Ạ.CẢM ƠN MNG NHIỀU🥺🥺🥺❤️😘😘😘

a:Xét ΔPBD vuông tại P và ΔMDB vuông tại M có
BD chung
góc PBD=góc MDB
Do đo: ΔPBD=ΔMDB
=>góc HBD=góc HDB
=>HB=HD
Xét tứ giác BHDK có
BH//DK
BK//DH
HB=HD
Do đó: BHDK là hình thoi
b: BHDK là hình thoi
nên HK là trung trực của BD(1)
ABCD là hình thoi
mà AC cắt BD tại O
nên O là trung điểm của BD(2), AC là trung trực của BD(3)
Từ (1), (2), (3) suy ra O,H,K,A,C thẳng hàng