
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(AH=\sqrt{15^2-9^2}=12\left(cm\right)\)
BI là phân giác của góc ABH
=>IA/AB=IH/BH
=>IA/5=IH/3=(IA+IH)/(5+3)=12/8=1,5
=>IA=7,5cm; IH=4,5cm
c: góc BAK+góc CAK=90 độ
góc BKA+góc HAK=90 độ
mà góc CAK=góc HAK
nên góc BAK=góc BKA
=>BI vuông góc AK
Xet ΔBAK có
BI,AI là đường cao
=>I là trực tâm
=>IK vuông góc AB
=>IK//AC

a: Xét ΔBAC có
D là trung điểm của AB
M là trung điểm của AC
Do đó: DM là đường trung bình của ΔABC
Suy ra: DM//BC và \(DM=\dfrac{BC}{2}=3.5\left(cm\right)\)

ΔAHC vuông tại H
=>AH^2+HC^2=AC^2
=>HC=3,2cm
Xét ΔAHC có AE là phân giác
nên HE/AH=EC/AC
=>HE/3=EC/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{HE}{3}=\dfrac{EC}{5}=\dfrac{HE+EC}{3+5}=\dfrac{3.2}{8}=0.4\)
=>HE=1,2cm

=x^4+1+2x^2+3x^3+3x+2x^2
=x^4+3x^3+4x^2+3x+2x^2
=x^3+x^3+2x^3+2x^2+2x^2+2x+x+1
=x^4+3x^3+4x^2+3x+1

Bài 3:
2) Ta có: \(B=2x\left(y-z\right)+\left(z-y\right)\left(x+t\right)\)
\(=2x\left(y-z\right)-\left(x+t\right)\left(y-z\right)\)
\(=\left(y-z\right)\left(x-t\right)\)
\(=\left(24-10,6\right)\left(18,3+31,7\right)\)
\(=13,4\cdot50=670\)
3) Ta có: \(C=\left(x-y\right)\left(y+z\right)+y\left(y-x\right)\)
\(=\left(x-y\right)\left(y+z\right)-y\left(x-y\right)\)
\(=z\left(x-y\right)\)
\(=1.5\left(0.86-0.26\right)\)
\(=0,9\)

Bài 4:
a: \(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\)
\(=2x^2+3x-10x-15-2x^2+6x+x+7\)
=-8
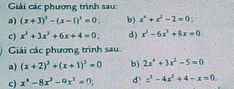

 Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
\(a,\left(x+3\right)^3-\left(x-1\right)^3=0\\ \Leftrightarrow\left(x^3+9x^2+27x+27\right)-\left(x^3-3x^2+3x-1\right)=0\\ \Leftrightarrow x^3+9x^2+27x+27-x^3+3x^2-3x+1=0\)
\(\Leftrightarrow12x^2+24x+28=0\\ \Leftrightarrow3x^2+6x+7=0\\ \Leftrightarrow9x^2+18x+21=0\\ \Leftrightarrow\left(3x\right)^2+2.3.3x+3^2+12=0\\ \Leftrightarrow\left(3x+3\right)^2+12=0\)
VÌ \(\left(3x+3\right)^2\ge0;12>0\Rightarrow\left(3x+3\right)^2+12>0\)
Vậy phương trình có tập nghiệm \(S=\varnothing\)
Tách nhỏ câu hỏi ra bạn