K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
25 tháng 12 2021
b/
\(\dfrac{x-3}{5}-\dfrac{x}{2}=\dfrac{3-x}{10}\)
\(\dfrac{x-3}{5}-\dfrac{x}{2}-\dfrac{3-x}{10}=0\)
\(\dfrac{-2x-9}{10}=0\)
\(-2x-9=0\)
\(\Rightarrow x=\dfrac{0+9}{-2}=\dfrac{-9}{2}\)
12 tháng 2 2022
a: Xét ΔABC có HG//BC
nên AH/HB=AG/GC(1)
Xét ΔADC có EG//DC
nên AG/GC=AE/ED(2)
Từ (1) và (2) suy ra AH/HB=AE/ED
hay HE//BD
b: Xét ΔABD có EH//BD
nên \(\dfrac{AE}{ED}=\dfrac{AH}{HB}\)
hay \(AE\cdot HB=AH\cdot ED\)
20 tháng 5 2020
( 2x - 1 ) - x = 0
=> 2x - 1 = x
=> 2x - x = 1
=> x = 1
( x - 1 )( 2x - 3) = 0
=> \(\orbr{\begin{cases}x-1=0\\2x-3=0\end{cases}}\)=> \(\orbr{\begin{cases}x=1\\x=\frac{3}{2}\end{cases}}\)
Vậy tập nghiệm của phương trình là S = { 1 ; 3/2 }
\(\frac{x}{x+1}=\frac{x+2}{x-1}\)( đkxđ : \(x\ne\pm1\))
( Chỗ này chưa học kĩ nên chưa hiểu lắm :]
11 tháng 12 2021
a: \(=\dfrac{x-8}{\left(x-2\right)\left(x+2\right)}+\dfrac{3}{2\left(x-2\right)}\)
\(=\dfrac{2x-16+3x+6}{\left(x-2\right)\left(x+2\right)\cdot2}=\dfrac{5}{2\left(x+2\right)}\)
21 tháng 12 2021
a: \(=\dfrac{2x\left(2x+1\right)}{\left(2x+1\right)^2}=\dfrac{2x}{2x+1}\)
T
13 tháng 9 2018
a) \(\Leftrightarrow\left(-63x^2+78x-15\right)+\left(63x^3+x-20\right)=44\)
\(\Leftrightarrow-63x^2+78x-15+63x^2+x-20=44\)
\(\Leftrightarrow79x-35=44\)
\(\Leftrightarrow79x=44+35\)
\(\Leftrightarrow79x=79\)
\(\Leftrightarrow x=1\)
b) \(\Leftrightarrow\left(x^2+3x+2\right).\left(x+5\right)-x^2.\left(x+8\right)=27\)
\(\Leftrightarrow x.\left(x^2+3x+2\right)+5.\left(x^2+3x+2\right)-x^3-8x^2=27\)
\(\Leftrightarrow x^3+3x^2+2x+5x^2+15x+10-x^3-8x^2=27\)
\(\Leftrightarrow17x+10=27\)
\(\Leftrightarrow17x=17\)
\(\Leftrightarrow x=1\)
19 tháng 12 2021
\(a,=\left(x-y\right)\left(x+y\right)+7\left(x-y\right)=\left(x+y+7\right)\left(x-y\right)\\ b,=\left(x-5\right)^2-9y^2=\left(x-3y-5\right)\left(x+3y-5\right)\)
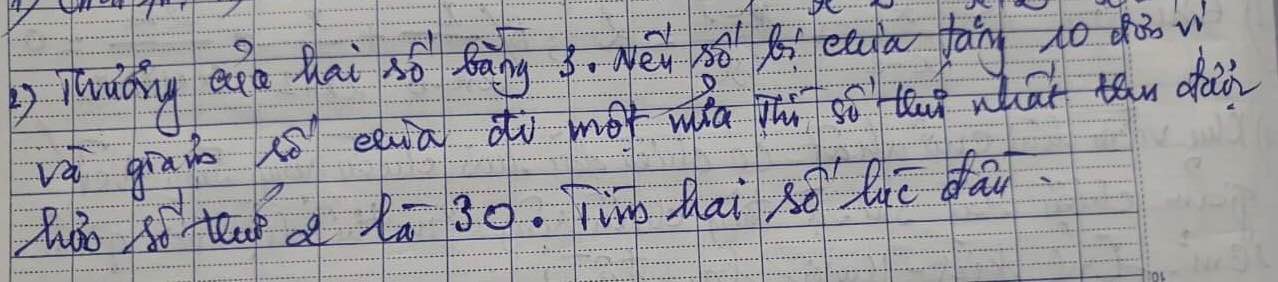
Gọi số bị chia, số chia ban đầu lần lượt là a,b.
=> a/b=3 (Với a khác b, a khác 0, b khác 0) (1)
Nếu số bị chia tăng 10 đơn vị và giảm số chia 1 nửa ta được:
=> (a+10)/0,5b = 3 - 30= -27 (2)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{b}=3\\\dfrac{a+10}{0,5b}=-27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a-3b=0\\a+13,5b=-10\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-16,5b=10\\a-3b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-1,65\\a-3.\left(-1,65\right)=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-1,65\\a=-4,95\end{matrix}\right.\)