Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ∆ABC và ∆A'B'C' ta có :
AB = A'B'
B'A'C' = BAC
AC = A'C'
=> ∆ABC = ∆A'B'C' (c.g.c)
b) Xét ∆AMC và ∆A'M'C' ta có :
AM = A'M'
BAC = B'A'C'
AC = A'C'
=> ∆AMC = ∆A'M'C' (c.g.c)
c) Ta có :
A'M' + M'B' = A'B'
AM + MB = AB
Mà AM = A'M' , A'B' = AB
=> BM = B'M
d) Vì ∆ABC = ∆A'B'C' (cmt)
=> ABC = A'B'C'
Xét ∆MBE và ∆M'B'E' ta có :
MB = M'B'
ABC = A'B'C'
BE = B'E'
=> ∆MBE = ∆M'B'E' (c.g.c)

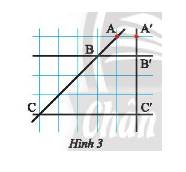
Ta xem độ dài một cạnh của hình vuông nhỏ là \(a\) và đường chéo của một hình vuông nhỏ là \(b\).
Khi đó, độ dài các đoạn thẳng là
\(AB = b;BC = 3b;A'B' = a;B'C' = 3a;AC = 4b;A'C' = 4a\)
a) Tỉ số của \(AB\) và \(BC\)là \(\frac{{AB}}{{BC}} = \frac{b}{{3b}} = \frac{1}{3}\).
Tỉ số của \(A'B'\) và \(B'C'\) là \(\frac{{A'B'}}{{B'C'}} = \frac{a}{{3a}} = \frac{1}{3}\).
Do đó, \(AB\) và \(BC\) tỉ lệ với \(A'B'\) và \(B'C'\).
b) Tỉ số của \(AC\) và \(A'C'\)là \(\frac{{AC}}{{A'C'}} = \frac{{4b}}{{4a}} = \frac{b}{a}\).
Tỉ số của \(AB\) và \(A'B'\) là \(\frac{{AB}}{{A'B'}} = \frac{b}{a}\).
Do đó, \(AC\) và \(A'C'\) tỉ lệ với \(AB\) và \(A'B'\).
Tùy zô tâm trạng cô giáo thui cậu !!! ^^