Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1 :
Vì ABCD là hình vuông \(\Rightarrow\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90^0\)
\(\Rightarrow AB=BC=CD=AD=4\)cm
Áp dụng định lí pytago tam giác ADC vuông tại D ta có :
\(AC^2=AD^2+CD^2=16+16=32\Rightarrow AC=4\sqrt{2}\)cm
Vì ABCD là hình vuông nên 2 đường chéo bằng nhau AC = BD = 4\(\sqrt{2}\)cm
Bài 2 :
Vì ABCD là hình chữ nhật nên \(AB=CD;AD=BC\)
Áp dụng định lí Pytago tam giác ACD vuông tại D ta có :
\(AC^2=AD^2+DC^2=27+9=36\Rightarrow AC=6\)cm

Gọi độ dài đg chéo là x (cm, x>0)
Vì đt hcn (chắc thế) => 1 góc vuông
Áp dụng Pytago: 6,82 + 142 = x2
=> x2 = 6056/25
=> x = căn 6056/5 (cm) (số xấu thế .-. t làm sai à)
=> Inches đt là: căn 6056/5 : 2,54 xấp xỉ 6,1 inch

Phạm Minh Hoàng, bạn có thể gửi tin nhắn cho mình và mình đưa câu hỏi này ra chỉ muốn bạn trả lời câu hỏi thôi. Mình mong bạn rút kinh nghiệm!!!!

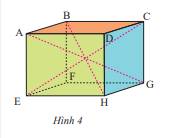
Ta có: AB = DC = EF = HG, mà DC = 5 cm nên AB = 5 cm
AD = BC = FG = EH, mà AD = 8 cm nên FG = 8 cm
AE = FB = DH = CG, mà DH = 6,5 cm nên AE = 6,5 cm

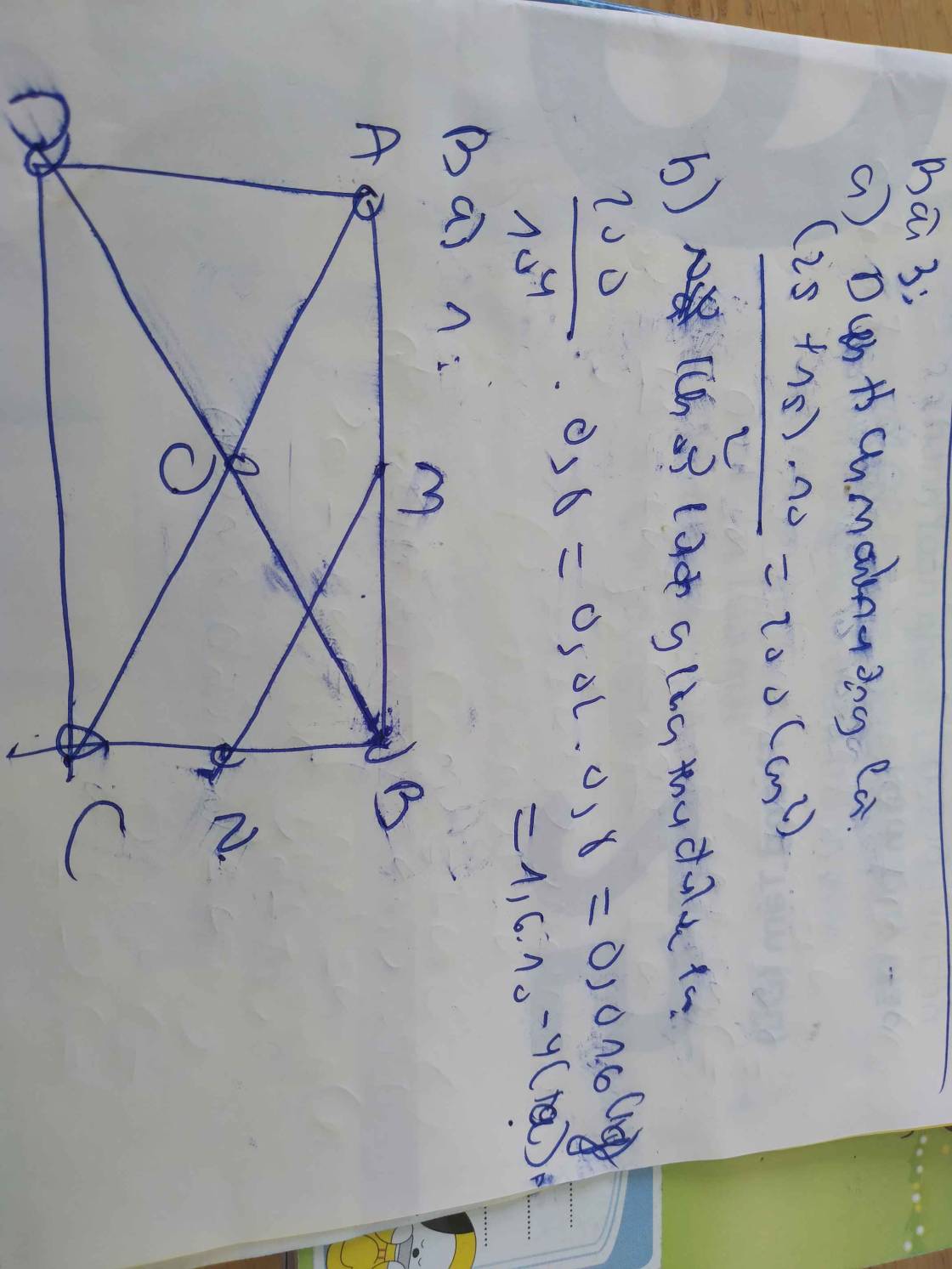

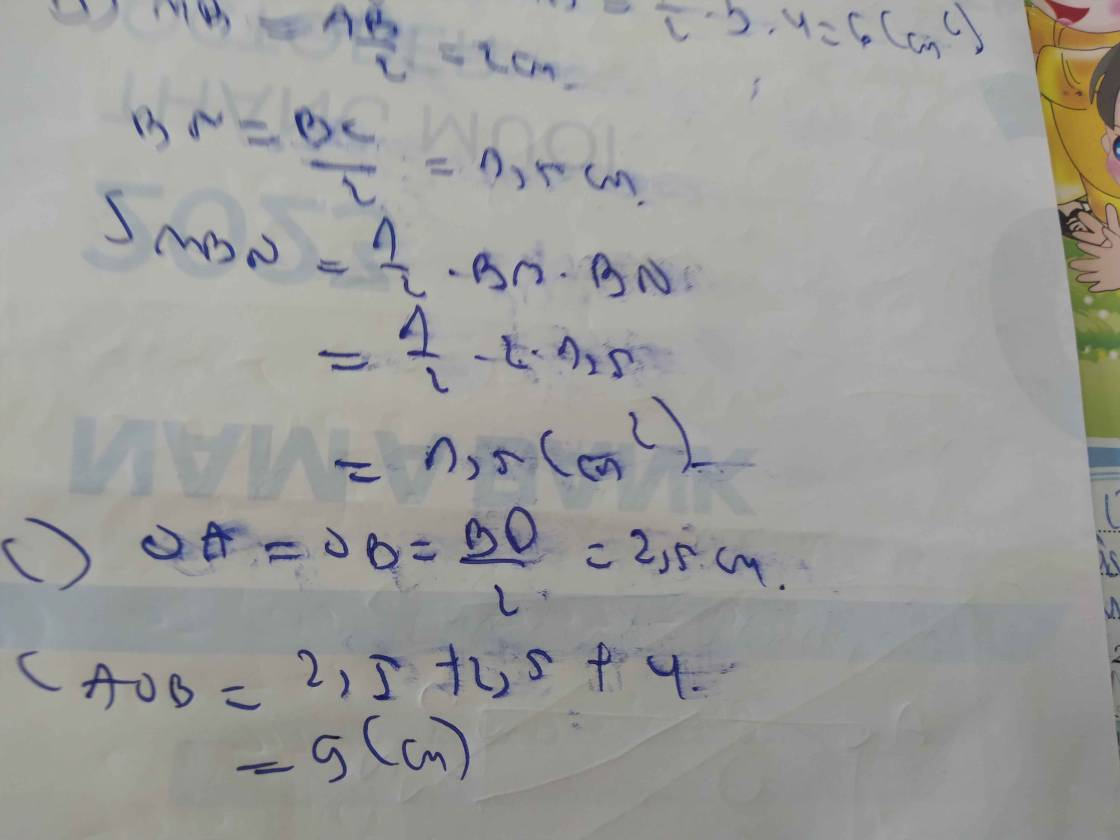
áp dụng đ/lí py-ta-go vào ΔABC, ta có:
\(AC^2=AB^2+BC^2\Leftrightarrow AC=\sqrt{AB^2+BC^2}\Leftrightarrow AC=\sqrt{8^2+6^2}=10\left(cm\right)\)
`AC` là đường chéo hình chữ nhật
Ta có: `AB^2 + BC^2 = AC^2`
`=> 64 + 36 = AC^2`
`=> AC = sqrt 100 = 10`.