Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Tại t = 0, i = 0,5I0 và đang tăng, dòng điện đổi chiều khi i = 0 A, tương ứng với:
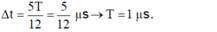
- Điện tích cực đại trên bản tụ:
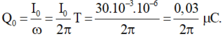

mình bị nhầm ở đáp án
A. \(\frac{4}{3}\mu s\) các câu khác cũng như vậy nhé
Năng lượng của mạch dao động W = \(\frac{Q_0^2}{2C}=\frac{LI^2_0}{2}\) → chu kì dao động của mạch
\(T=2\pi\sqrt{LC}=2\pi\frac{Q_0}{I_0}=16.10^{-6}\left(s\right)=16\mu s\).Thời gian điện tích giảm từ Q0 dến Q0/2
q = Q0cos \(\frac{2\pi}{T}t=\frac{Q_0}{2}\rightarrow\frac{2\pi}{T}t=\frac{\pi}{3}\rightarrow t=\frac{T}{6}=\frac{8}{3}\mu s\)
→ C

+ Tại t = 0, i = 0 , 5 I 0 và đang tăng, dòng điện đổi chiều khi i = 0A, tương ứng với

Đáp án C

Sau khoảng thời gian ngắn nhất \(0,25 \mu s\) năng lượng điện trường và năng lượng từ trường => \(\frac{T}{4}= 0,25 \mu s=> T = 10^{-6}s=> \omega = \frac{2\pi}{T}= 2\pi.10^{6}(rad/s).\)
\(q_0 = \frac{I_0}{\omega} = \frac{2.10^{-8}}{\pi}C.\)
\(W_L=W_C = \frac{0,8}{\pi}.10^{-6}=> q = \pm \frac{q_0}{\sqrt{2}}.\)
Ta có: \(\frac{1}{2}\frac{q_0^2}{2C}=\frac{0,8}{\pi}.10^{-6}=> C = \frac{1,25.10^{-10}}{\pi}F = \frac{125}{\pi}pF.\)
bạn giải đúng rồi nhưng mà đoạn cuối công thức là (1/2)*(q02/C) chứ ko phải là 2C. đáp án là D

Cứ sau những khoảng thời gian \(\frac{T}{4}\) s thì năng lượng trong tụ điện và trong cuộn cảm lại bằng nhau.
\(=> \frac{T}{4}=1\mu s=> T = 4.10^{-6}s.\)
\(W_{Cmax} = \frac{1}{2}CU_0^2=> C = \frac{2W_{Cmax}}{U_0^2} = 1,25.10^{-7}F.\)
\(T = 2\pi .\sqrt{LC}=> L = \frac{T^2}{4\pi^2C}=\frac{32}{\pi^2}\mu H.\)


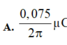
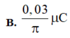
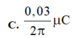
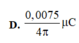

Dòng điện đổi chiều khi dòng điện đi qua VTCB.
Vẽ đường tròn tương ứng
Vị trí ban đầu ứng với pha ban đầu là \(-\frac{\pi}{3}\) ứng với điểm N.
Vị trí gần nhất (quay theo chiều ngược chiều kim đồng hồ) thì điểm N là vị trí gần nhất tại đó dòng đổi chiều.
\(t=\frac{\varphi}{\omega}=\frac{5\pi}{6}\Rightarrow\omega=\frac{5\pi}{6}:t=2\pi.10^6\)
Điện tích cực đại \(Q_o=\frac{I_0}{\omega}=\frac{30}{2\pi.10^6}=\frac{1,5.10^{-5}}{\pi}C\)
Như vậy đáp án C thỏa mãn.