
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(5^{\log_{125}64}=5^{\log_{5^3}64}=5^{\dfrac{1}{3}\log_564}=5^{\log_564^{\dfrac{1}{3}}}=5^{\log_5\sqrt[3]{64}}=5^{\log_54}=4\)
\(=5^{log_{5^3}64}=5^{\dfrac{1}{3}\cdot log_564}\)
\(=5^{log_5\sqrt[3]{64}}=5^{log_54}=4\)

\(2\sqrt{3}=\sqrt{12}< \sqrt{18}=3\sqrt{2}\)
=>\(2^{2\sqrt{3}}< 2^{3\sqrt{2}}\)

a: \(=\dfrac{5}{4}\cdot3=\dfrac{15}{4}\)
b: \(=\sqrt[5]{\dfrac{98}{64}\cdot343}=\sqrt[5]{\left(\dfrac{7}{2}\right)^5}=\dfrac{7}{2}\)

\(pH=-log\left[H^+\right]=-log\left[10^{-4}\right]=4\)
\(pH=-log\left[H^+\right]=-log\left[10^{-5}\right]=5\)

Số vận động viên được khảo sát là \(n = 3 + 8 + 12 + 12 + 4 = 39\).
Gọi \({x_1};{x_2};...;{x_{39}}\) là thời gian luyện tập của 39 vận động viên được xếp theo thứ tự không giảm. Ta phải chọn các vận động viên có thời gian luyện tập tương ứng là \({x_{30}};{x_{31}};...;{x_{39}}\)
Ta có:
\({x_1},{x_2},{x_3} \in \left[ {0;2} \right);{x_4},...,{x_{11}} \in \left[ {2;4} \right);{x_{12}},...,{x_{23}} \in \left[ {4;6} \right);{x_{24}},...,{x_{35}} \in \left[ {6;8} \right);{x_{36}},...,{x_{39}} \in \left[ {8;10} \right)\). Vậy \({x_{30}}\) thuộc nhóm \(\begin{array}{*{20}{l}}{\left[ {6;8} \right)}\end{array}\).
Ta có: \(n = 29;{n_j} = 12;C = 3 + 8 + 12 = 23;{u_j} = 6;{u_{j + 1}} = 8\)
\({x_{30}} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 6 + \frac{{\frac{{3.39}}{4} - 23}}{{12}}.\left( {8 - 6} \right) \approx 7,04\)
Vậy huấn luyện viên nên chọn các vận động viên có thời gian luyện tập từ 7,04 giờ trở lên.

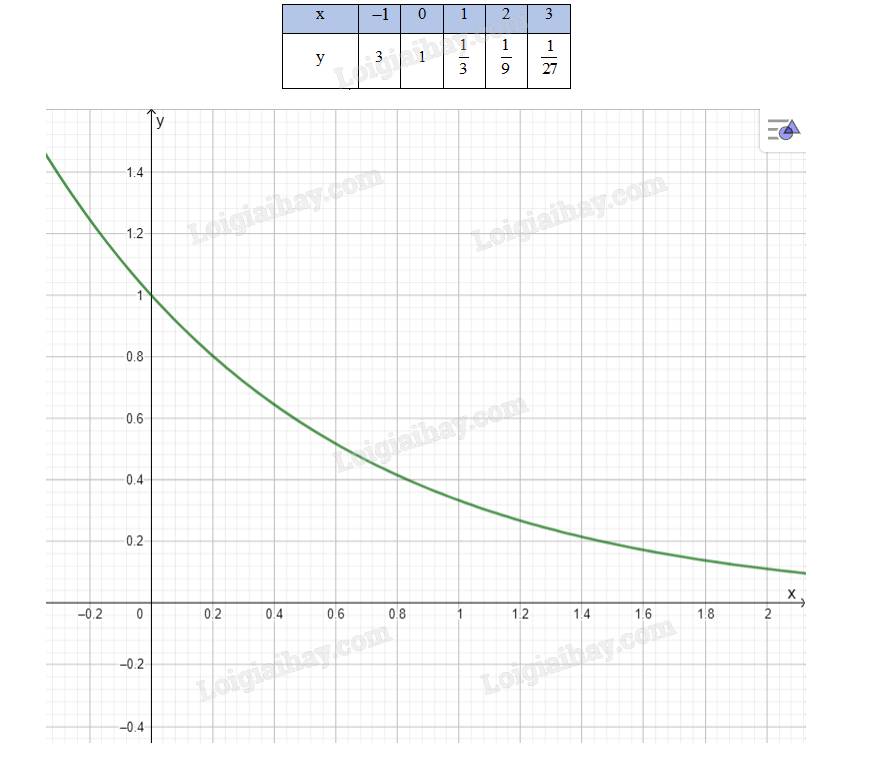
\(\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{1}{3}} \right)^x} = 0;\,\,\mathop {\lim }\limits_{x \to - \infty } {\left( {\frac{1}{3}} \right)^x} = + \infty \)
Hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) nghịch biến trên toàn R
Bảng biến thiên của hàm số:

Đồ thị hàm số:

\(=log_35^2-log_350+log_36\)
\(=log_3\left(\dfrac{25}{50}\cdot6\right)=log_33=1\)


2;-2 là căn bậc 6 của 64 vì \(2^6=64;\left(-2\right)^6=64\)