Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi độ dài quãng đường AB là x (đơn vị km, x > 0)
Thời gian ô tô tải đi từ A đến B là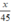 
(giờ)
Thời gian xe con đi từ A đến B là 
(giờ)
Vì xe con xuất phát sau xe tải 1 giờ 30 phút =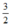 
giờ nên ta có phương trình:
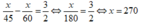
(thỏa mãn điều kiện)
Vậy độ dài quãng đường AB là 270km.
Chọn đáp án A
Tổng cả ba vận tốc của hai xe là
\(30+10+60=100\) km/giờ
Thời gian của hai xe là
2 giờ + 30 phút \(=2\) giờ \(30\) phút
Đổi 2 giờ 30 phút \(=2,5\) giờ
Quãng đường AB dài số km là
\(100\times2,5=250\) km
Đáp số 250 km
Chúc bạn học giỏi
Bài 2:
Gọi độ dài quãng đường AB là \(x\left(km\right),x>0\).
Thời gian xe tải đi từ A đến B là: \(\frac{x}{30}\left(h\right)\).
Thời gian xe con đi từ A đến B là: \(\frac{\frac{3}{4}x}{45}+\frac{\frac{1}{4}x}{50}=\frac{13x}{600}\left(h\right)\)
Đổi: \(2h20'=\frac{7}{3}h\).
Ta có phương trình: \(\frac{x}{30}-\frac{13x}{600}=\frac{7}{3}\)
\(\Leftrightarrow x=200\)(thỏa mãn)
Gọi độ dài quãng đường AB là \(x\left(km\right),x>0\).
Đổi: nửa giờ \(=\)\(0,5h\), \(40'=\frac{2}{3}h\).
Thời gian xe con đi từ A đến B là: \(\frac{x}{60}+\frac{2}{3}\left(h\right)\).
Thời gian xe tải đi từ A đến B là: \(\frac{\frac{x}{2}}{40}+\frac{\frac{x}{2}}{50}=\frac{9x}{400}\left(h\right)\).
Ta có: \(\frac{9x}{400}-\left(\frac{x}{60}+\frac{2}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow x=200\)(thỏa mãn)
Gọi quãng đường AB là x (km). Điều kiện x > 0
Thời gian xe tải đi từ A đến B là x/30 (giờ).
Thời gian xe ô tô đi từ A đến B là x/40 (giờ).
Vì ô tô đi sau một giờ và đuổi kịp xe tải tại B nên ta có phương trình:
(x/30) - (x/40) = 1 ⇔ 4x - 3x = 120 ⇔ x = 120 (thỏa mãn điều kiện)
Vậy quãng đường AB dài 120 km.
Study well...
Gọi quãng đường AB là x (km). Điều kiện x > 0
Thời gian xe tải đi từ A đến B là x/30 (giờ).
Thời gian xe ô tô đi từ A đến B là x/40 (giờ).
Vì ô tô đi sau một giờ và đuổi kịp xe tải tại B nên ta có phương trình:
(x/30) – (x/40) = 1 ⇔ 4x – 3x = 120 ⇔ x = 120 (thỏa mãn điều kiện)
Vậy quãng đường AB dài 120 km.
Gọi quãng đường AB là x (km)
Thời gian sau khi xe con xuất phát sau là: t (giờ)
Thời gian xe tải đi hết quãng đường AB là: \(\frac{x}{45}\) (giờ)
Thời gian ô tô đi hết quãng đường AB là: \(\frac{x}{60}\)(giờ)
Vì sau t(giờ ) ô tô sẽ đuổi kịp xe tải nên ta có phương trình:
\(\frac{x}{45}=\frac{x}{60}+t\Rightarrow t-\frac{x}{180}=0\left(1\right)\)
Thời gian xe tải đi đến lúc gặp nhau thực tế là:
\(t+\frac{x}{2.60}+1\)
Quãng đường xe tải đi được khi đó là:
\(45.\left(t+\frac{x}{2.60}+1\right)\)
Vì sau khi đi được nửa quãng đường ab thì ô tô tăng vận tốc lên 75km/h, nên sau đó 1 giờ thì đuổi kịp xe tải nên ta có phương trình:
\(45.\left(t+\frac{x}{2.60}+1\right)=\frac{x}{2}+75.1\)
\(45t-\frac{x}{8}=30\)
Từ (1) và (2) ta có hệ phương trình:
\(\hept{\begin{cases}t-\frac{x}{180}=0\\45t-\frac{x}{8}=30\end{cases}}\)
Giải hệ phương trình ta được
\(\hept{\begin{cases}t=\frac{4}{3}\\x=240\end{cases}}\)
vậy quãng đường AB dài 240 km.
Nếu xe con ở chính giữa 2 xe máy và xe tải thì khoảng cách giữa xe con với xe máy và xe con và xe tải là bằng nhau
Trong 2 giờ xe máy đi được 30 x 2 = 60 km
Trong 2 giờ xe tải đi được 50 x 2 = 100 km
=> Hiệu vận tốc xe con với xe máy là : 60 - 30 = 30 km/h
=> Sau 60 : 30 = 2 giờ thì vị trí của xe con ngang với vị trí xe máy và lúc đó vào 6 giờ + 2 giờ + 2 giờ = 10 giờ
=> Lúc 10 giờ xe máy và xe con đều đã đi được 60 x 2 = 120 km như nhau
=> Trong 2 giờ đó tiếp theo xe tải đi được 50 x 2 = 100 km
và xe tải đã đi được 100 + 100 = 200 km
xét từng trường hợp
Trường hợp 1 : từ 1 giờ sau đó
=> xe máy đi được 120 + 30 x 1 = 150 km
=> xe con đi được : 120 + 60 x 1 = 180 km
=> xe tải đi được : 200 + 50 x 1 = 250 km
ta có 180 - 150 < 250 - 180 => loại
Trường hợp 2 : từ 2 giờ sau đó
=> xe máy đi được 120 + 30 x 2 = 180 km
=> xe con đi được : 120 + 60 x 2 = 240 km
=> xe tải đi được : 200 + 50 x 2 = 300 km
ta có 240 - 180 = 300 - 240 = 60 => chọn
=> sau 2 giờ thì xe con ở chính giữa xe máy và xe tải
=> lúc đó là 10 giờ + 2 giờ = 12 giờ