Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
+ Độ giãn của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 100 = 1 cm.
Tần số góc dao động của con lắc ω = k m = 10 10 rad/s.
+ Vận tốc truyền cho vật m so với điểm treo có độ lớn v 0 = 10 + 40 = 50 cm/s.
→ Biên độ dao động của vật sau đó A = v 0 ω = 50 10 10 = 1 , 58 cm.
→ Chiều dài cực đại l m a x = l 0 + Δ l 0 + A = 27 , 58 c m .
\(\Delta l=\frac{g}{\omega^2}=0,25m\)
\(t=0\Rightarrow x=5\sqrt{3}cm\Rightarrow l=l_0+\Delta l+x=158,66cm\)
Vậy không phương án đúng
Chọn C
+ 
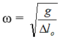= 20 => Δlo = 0,025m = 2,5cm.
+ lCB = lo + Δlo = 30 + 2,5 = 32,5 cm.
Hướng dẫn:
+ Tần số góc của dao động ω = k m = 10 π rad/s.
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 1 c m
+ Khi vật đang ở vị trí có li độ x = –1 cm → l = l 0 = 40 c m , người ta tiến hành giữ cố định lò xo tại điểm cách điểm cố định 20 cm → lò xo mới tham gia vào dao động có độ cứng k' = 2k = 200 N/m.
+ Năng lượng của con lắc trước khi cố định lò xo: E t = k x 2 = 0 , 01 E d = 1 2 k A 2 − x 2 = 0 , 035 J
→ Năng lượng của hệ sau cố định lò xo đúng bằng tổng động năng và một nửa thế năng của vật trước khi cố định lò xo.
E ' = 0 , 5 k A ' 2 = E d + 0 , 5 E t = 0 , 04 J → A' = 0,02 cm.
→ Lực đàn hồi cực đại F m a x = k ' ( 0 , 5 Δ l 0 + A ' ) = 6 N .
Đáp án B
Đáp án A
Phương pháp: Áp dụng công thức chiều dài nhỏ nhất và lớn nhất của con lắc lò xo treo thẳng đứng
Cách giải :
Ở VTCB lò xo dãn một đoạn:
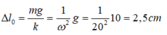
Khi ở VTCB lò xo có chiều dài: l c b = 30 + 2,5 = 32,5 cm
Biên độ dao động A = 2 cm nên chiều dài nhỏ nhất và lớn nhất lần lượt là
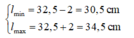
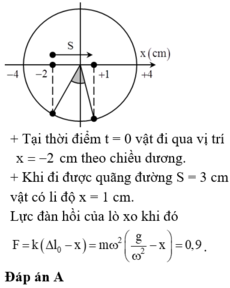
Chiều dương trục toạ độ hướng lên thì chiều dài lò xo là:
\(\ell=\ell_0+\Delta\ell_0-x\)
\(\omega=\sqrt{\dfrac{g}{\Delta \ell_0}}\Rightarrow \Delta\ell_0=0,1m=10cm.\)
Thay \(t=0,75T\) vào PT dao động ta tìm được \(x=2\sqrt 3\)(cm)
Vậy: \(\ell=60+10-2\sqrt3\approx 66,5\) cm.
Chọn B.