K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
3 tháng 10 2021
a) \(2^4+8\left[\left(-2\right)^2:\dfrac{1}{2}\right]^0-2^{-2}.4+\left(-2\right)^2\)
\(=2^4+8.1-\dfrac{1}{4}.4+4\)
\(=16+8-1+4\)
\(=24-1+4\)
\(=23+4\)
\(=27\)
LL
0
LL
1
24 tháng 9 2015
\(\frac{3}{14}:\frac{1}{28}-\frac{13}{21}:\frac{1}{28}+\frac{29}{42}:\frac{1}{28}-8\)
\(=\left(\frac{3}{14}-\frac{13}{21}+\frac{29}{42}\right):\frac{1}{28}-8\)
\(=\left(\frac{9}{42}-\frac{26}{21}+\frac{29}{42}\right):\frac{1}{28}-8\)
\(=\left(\frac{-17}{42}+\frac{29}{42}\right):\frac{1}{28}-8\)
\(=\frac{12}{42}:\frac{1}{28}-8\)
\(=\frac{2}{7}.28-8\)
\(=\frac{56}{7}-8\)
\(=8-8\)
\(=0\)
24 tháng 4 2020
\(x\left(x-\frac{1}{3}\right)< 0\)
Để \(x\left(x-\frac{1}{3}\right)< 0\)thì x và \(x-\frac{1}{3}\)trái dấu nhau
Thấy \(x>x-\frac{1}{3}\)\(\Rightarrow\hept{\begin{cases}x>0\\x-\frac{1}{3}< 0\end{cases}\Rightarrow\hept{\begin{cases}x>0\\x< \frac{1}{3}\end{cases}\Leftrightarrow}0< x< \frac{1}{3}}\)
11 tháng 10 2021
Bài 4:
Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\)
nên \(\dfrac{a}{c}=\dfrac{b}{d}\)
\(\Leftrightarrow\dfrac{c}{a}=\dfrac{d}{b}\)
hay \(\dfrac{a+c}{a}=\dfrac{b+d}{b}\)
H9
HT.Phong (9A5)
CTVHS
1 tháng 7 2023
Bài 8:
a) \(\left(-3,5\right):\left(-2\dfrac{3}{5}\right)=\dfrac{7}{2}:\dfrac{13}{2}=\dfrac{7}{2}\cdot\dfrac{2}{13}=\dfrac{7\cdot2}{2\cdot13}=\dfrac{7}{13}\)
b) \(\left(-\dfrac{11}{15}\right):1\dfrac{1}{10}=\left(-\dfrac{11}{15}\right):\dfrac{11}{10}=\left(-\dfrac{11}{15}\right)\cdot\dfrac{10}{11}=\dfrac{-11\cdot10}{15\cdot11}=-\dfrac{10}{15}=-\dfrac{2}{3}\)
c) \(2\dfrac{2}{3}:\left(-3\dfrac{3}{4}\right)=\dfrac{8}{3}:-\dfrac{15}{4}=\dfrac{8}{3}\cdot-\dfrac{4}{15}=\dfrac{8\cdot4}{3\cdot15}=-\dfrac{32}{45}\)
H9
HT.Phong (9A5)
CTVHS
1 tháng 7 2023
Bài 7:
a) \(\left(-\dfrac{3}{25}\right):6=\left(-\dfrac{3}{25}\right)\cdot\dfrac{1}{6}=\dfrac{-3\cdot1}{25\cdot6}=-\dfrac{1}{50}\)
b) \(-\dfrac{5}{23}:-2=\dfrac{5}{23}\cdot\dfrac{1}{2}=\dfrac{5\cdot1}{23\cdot2}=\dfrac{5}{26}\)
c) \(\dfrac{-7}{11}:-3,5=\dfrac{7}{11}:\dfrac{7}{2}=\dfrac{7}{11}\cdot\dfrac{2}{7}=\dfrac{7\cdot2}{11\cdot7}=\dfrac{2}{11}\)
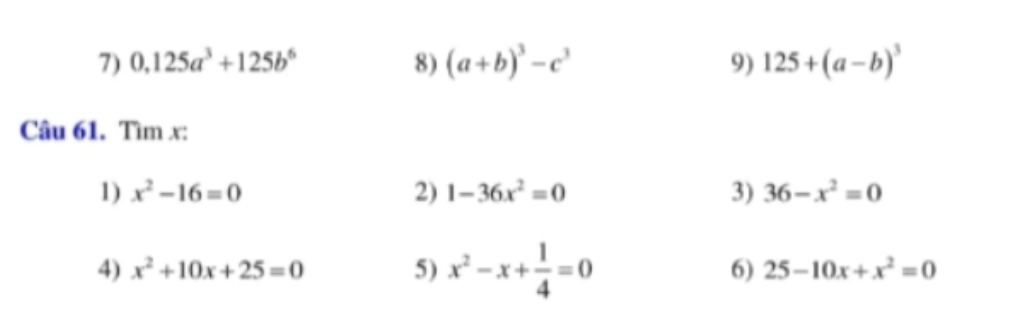
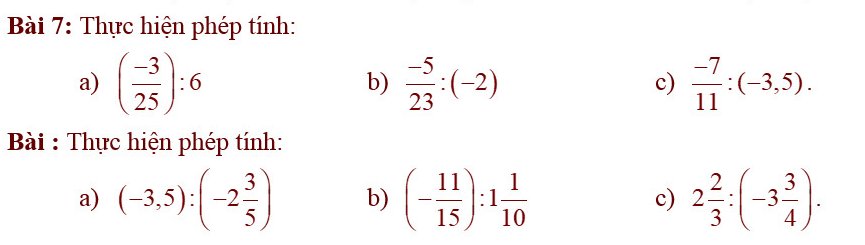
1: Ta có: \(x^2-16=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
2: Ta có: \(1-36x^2=0\)
\(\Leftrightarrow\left(6x-1\right)\left(6x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{6}\\x=-\dfrac{1}{6}\end{matrix}\right.\)
\(7,=\left(0,5a+5b\right)\left(0,25a^2-2,5ab+25b^2\right)\\ 8,=\left(a+b-c\right)\left(a^2+2ab+b^2+ac+bc+c^2\right)\\ 9,=\left(5+a-b\right)\left(25-5a+5b+a^2-2ab+b^2\right)\)
\(61,\\ 1,\Leftrightarrow\left(x-4\right)\left(x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\\ 2,\Leftrightarrow\left(1-6x\right)\left(1+6x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{6}\\x=-\dfrac{1}{6}\end{matrix}\right.\\ 3,\Leftrightarrow\left(6-x\right)\left(6+x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)