
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(=\dfrac{\left(3n-2\right)-m\left(3n-2\right)}{\left(1-m\right)^3}=\dfrac{3n-2}{\left(1-m\right)^2}\)

\(1,P=2x^2-2y^2-x^2+2xy-y^2+x^2+2xy+y^2-4y^2\\ P=2x^2-6y^2+4xy\\ 2,\\ a,=x\left(x-y\right)+3\left(x-y\right)=\left(x+3\right)\left(x-y\right)\\ b,=x\left(x^2-4x-y^2+4\right)\\ =x\left[\left(x-2\right)^2-y^2\right]=x\left(x-y-2\right)\left(x+y-2\right)\\ c,=\left[\left(x+1\right)\left(x+4\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]-3\\ =\left(x^2+5x+4\right)\left(x^2+5x+6\right)-3\\ =\left(x^2+5x+5-1\right)\left(x^2+5x+5+1\right)-3\\ =\left(x^2+5x+5\right)^2-1-3\\ =\left(x^2+5x+5\right)^2-4\\ =\left(x^2+5x+5+2\right)\left(x^2+5x+5-2\right)=\left(x^2+5x+7\right)\left(x^2+5x+3\right)\)

ΔAHC vuông tại H
=>AH^2+HC^2=AC^2
=>HC=3,2cm
Xét ΔAHC có AE là phân giác
nên HE/AH=EC/AC
=>HE/3=EC/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{HE}{3}=\dfrac{EC}{5}=\dfrac{HE+EC}{3+5}=\dfrac{3.2}{8}=0.4\)
=>HE=1,2cm

a) cm tam giác AKC và tam giác AHC bằng nhau TH cạnh huyền góc nhọn
b) cm tam giác HAK là tam giác cân (có đg trung tuyến là đường cao)
cm tam giác HAK có 1 góc = 60o => tam giác HAK đều
Cạnh huyền là AC
Góc nhọn là KCA và HCA nhé
b) Từ 2 tam giác bằng nhau đã chứng minh ở câu a (*)=> KAC^ = HAC^ (2 góc t/ứng) => AC là tia phân giác của tam giác HAK
=> AK = AH => tg HAK cân tại A (1)
.....
cm 1 góc của HAK = 60o vì tam giác cân có 1 góc = 60o là tam giác đều nha ^^!
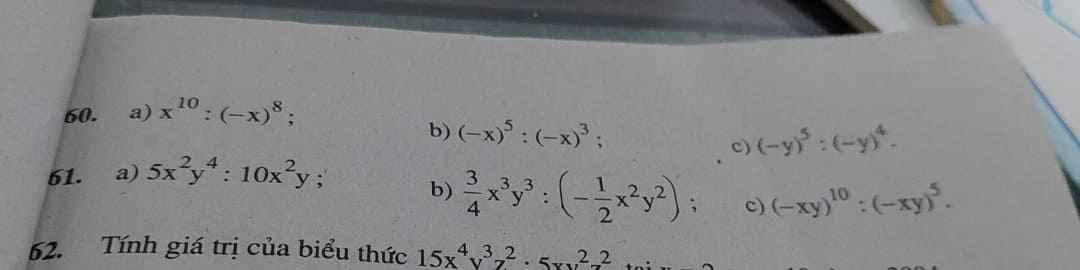 lm giup em 60 61 thoi ah em xin day ah
lm giup em 60 61 thoi ah em xin day ah
Bài 60:
a) \(x^{10}:\left(-x\right)^8=x^{10}:x^8=x^2\)
b) \(\left(-x\right)^5:\left(-x\right)^3=\left(-x\right)^2=x^2\)
c) \(\left(-y\right)^5:\left(-y\right)^4=-y\)
Bài 61:
a) \(5x^2y^4:10x^2y=\dfrac{1}{2}y^3\)
b) \(\dfrac{3}{4}x^3y^3:\left(-\dfrac{1}{2}x^2y^2\right)=-\dfrac{3}{2}xy\)
c) \(\left(-xy\right)^{10}:\left(-xy\right)^5=\left(-xy\right)^5=-x^5y^5\)