Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{3x^2+2}-\sqrt{4+x}}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{3x^2-x-2}{\sqrt{3x^2+2}+\sqrt{4+x}}}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{3x+2}{\left(x+1\right)\left(\sqrt{3x^2+2}+\sqrt{4+x}\right)}=\dfrac{5}{2.2\sqrt{5}}=\dfrac{\sqrt{5}}{4}\).
Từ đó a = 5; b = 4 nên a - b = 1.

\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{3x+1}-2}{x^2-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{3x+1-4}{\sqrt{3x+1}+2}\cdot\dfrac{1}{x^2-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{3x-3}{\left(x-1\right)\left(x+1\right)\left(\sqrt{3x+1}+2\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{3}{\left(x+1\right)\left(\sqrt{3x+1}+2\right)}=\dfrac{3}{\left(1+1\right)\left(\sqrt{3+1}+2\right)}\)
\(=\dfrac{3}{2\cdot4}=\dfrac{3}{8}\)
=>a=3;b=8
=>a2+b=9+8=17

\(a+\dfrac{x+1}{\sqrt{x^2-x+1}}-\dfrac{3x+3}{\sqrt{x}}=0\) có nghiệm \(x=1\)
\(\Rightarrow a+\dfrac{2}{\sqrt{1}}-\dfrac{6}{\sqrt{1}}=0\Rightarrow a=4\)
\(4+\dfrac{x+1}{\sqrt{x^2-x+1}}-\dfrac{3x+3}{\sqrt{x}}=3\left(2-\dfrac{x+1}{\sqrt{x}}\right)+\left(\dfrac{x+1}{\sqrt{x^2-x+1}}-2\right)\)
\(=-3\left(\dfrac{\left(x-1\right)^2}{\sqrt{x}\left(x+1+2\sqrt{x}\right)}\right)+\dfrac{-3\left(x-1\right)^2}{\sqrt{x^2-x+1}\left(x+1-2\sqrt{x^2-x+1}\right)}\)
Rút gọn với \(\left(x-1\right)^2\) bên ngoài rồi thay dố là được

\(\lim\limits_{x\rightarrow0}\dfrac{x}{\sqrt[7]{x+1}\left(\sqrt[]{x+4}-2\right)+2\left(\sqrt[7]{x+1}-1\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{x}{\dfrac{x\sqrt[7]{x+1}}{\sqrt[]{x+4}+2}+\dfrac{2x}{\sqrt[7]{\left(x+1\right)^6}+\sqrt[7]{\left(x+1\right)^5}+\sqrt[7]{\left(x+1\right)^4}+\sqrt[7]{\left(x+1\right)^3}+\sqrt[7]{\left(x+1\right)^2}+\sqrt[7]{x+1}+1}}\)
\(=\dfrac{1}{\dfrac{1}{2+2}+\dfrac{2}{1+1+1+1+1+1+1}}=\dfrac{28}{15}\)



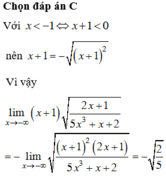
Chọn A
*Ta có:
* Xét hàm số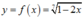 ta có
ta có 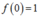 .
.
Theo định nghĩa đạo hàm ta có: