Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)` Gọi đường thẳng `\Delta` song song với `d` là: `3x+4y+c=0` `(c ne 5)`
Mà `I in \Delta`
`=>2.1+4.3+c=0<=>c=-14` (t/m)
`=>PTTQ` của `\Delta` là: `3x+4y-14=0`
`b)` Có: `R=d(I;d)=[|3.1+4.3+5|]/[\sqrt{3^2+4^2}]=4`
`=>` Ptr đường tròn tâm `I` bán kinh `R=4` là:
`(x-1)^2+(y-3)^2=16`

1.
Gọi \(I\left(x;y\right)\) là tâm đường tròn \(\Rightarrow\overrightarrow{AI}=\left(x-1;y-3\right)\)
Do đường tròn tiếp xúc với \(d_1;d_2\) nên:
\(d\left(I;d_1\right)=d\left(I;d_2\right)\Rightarrow\dfrac{\left|5x+y-3\right|}{\sqrt{26}}=\dfrac{\left|2x-7y+1\right|}{\sqrt{53}}\)
Chà, đề đúng ko em nhỉ, thế này thì vẫn làm được nhưng rõ ràng nhìn 2 cái mẫu kia thì số liệu sẽ xấu 1 cách vô lý.
2.
Phương trình đường thẳng kia là gì nhỉ? \(2x+y=0\) à?

Tham khảo :
mk tham khảo nên ko chắc đúng
\(Đáp án: ( x − 1 2 ) 2 + ( y − 3 2 ) 2 = 25 2 Giải thích các bước giải: Tọa độ giao điểm của (d) và (C) là nghiệm của hệ phương trình { x − 7 y + 10 = 0 x 2 + y 2 − 2 x + 4 y − 20 = 0 ⇔ { x = 7 y − 10 ( 1 ) x 2 + y 2 − 2 x + 4 y − 20 = 0 ( 2 ) Thay (1) vào (2) ta được ( 7 y − 10 ) 2 + y 2 − 2 ( 7 y − 10 ) + 4 y − 20 = 0 ⇔ 49 y 2 − 140 y + 100 + y 2 − 14 y + 20 + 4 y − 20 = 0 ⇔ 50 y 2 − 150 y + 100 = 0 ⇔ y 2 − 3 y + 2 = 0 ⇔ ( y − 2 ) ( y − 1 ) = 0 ⇔ [ y = 2 y = 1 + ) y = 2 ⇒ x = 4 ⇒ B ( 4 ; 2 ) + ) y = 1 ⇒ x = − 3 ⇒ C ( − 3 ; 1 ) Phương trình đường tròn có dạng ( C 1 ) x 2 + y 2 − 2 a x − 2 b y + c = 0 Ta có đường tròn đi qua 3 điểm A ( 1 ; − 2 ) , B ( 4 ; 2 ) , C ( − 3 ; 1 ) A ( 1 ; − 2 ) ∈ ( C 1 ) : 1 2 + ( − 2 ) 2 − 2 a + 4 b + c = 0 ⇔ − 2 a + 4 b + c = − 5 B ( 4 ; 2 ) ∈ ( C 1 ) : 4 2 + 2 2 − 8 a − 4 b + c = 0 ⇔ − 8 a − 4 b + c = − 20 C ( − 3 ; 1 ) ∈ ( C 1 ) : ( − 3 ) 2 + 1 2 + 6 a − 2 b + c = 0 ⇔ 6 a − 2 b + c = − 10 Ta có hệ phương trình ⎧ ⎨ ⎩ − 2 a + 4 b + c = − 5 − 8 a − 4 b + c = − 20 6 a − 2 b + c = − 10 ⇔ ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ a = 1 2 b = 3 2 c = − 10 ⇒ I ( 1 2 ; 3 2 ) , R = √ 1 2 2 + 3 2 2 − ( − 10 ) = 5 √ 2 2 Phương trình đường tròn có dạng ( x − 1 2 ) 2 + ( y − 3 2 ) 2 = 25 2 \)

Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
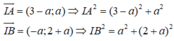
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
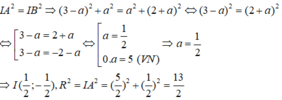
Vậy phương trình đường tròn có dạng:
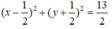
Ta có:
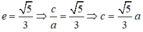
Giả sử elip (E) có dạng:
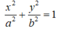
Vì (E) đi qua B nên:
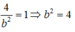
Mà
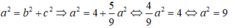
Vậy phương trình chính tắc của elip (E) là:
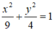

1.
Trục Ox có pt \(y=0\) nên đường song song với nó là \(y=4\)
2.
\(\overrightarrow{MI}=\left(1;-2\right)\)
Đường thẳng tiếp xúc với đường tròn tâm I tại M đi qua M và vuông góc MI nên nhận \(\overrightarrow{MI}\) là 1 vtpt
Phương trình:
\(1\left(x-1\right)-2\left(y-3\right)=0\Leftrightarrow x-2y+5=0\)
Lập phương trình đường tròn đi qua 2 điểm A(–1;3), B(1;5) và có tâm nằm trên đường thẳng ∆:3x-y-4=0.

Tâm I nằm trên Δ nên I(x;3x-4)
IA=IB
=>(x+1)^2+(3x-4-3)^2=(x-1)^2+(3x-9)^2
=>x^2+2x+1+9x^2-42x+49=x^2-2x+1+9x^2-54x+81
=>-40x+50=-56x+82
=>16x=32
=>x=2
=>I(2;2)
R=IA=căn (2+1)^2+(3-2)^2=căn 10
(C): (x-2)^2+(y-2)^2=10
Do đường tròn (C) đi qua M, N nên tâm I của đường tròn nằm trên trung trực của MN
Gọi P là trung điểm MN \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{NM}=\left(1;-2\right)\\P\left(\dfrac{3}{2};2\right)\end{matrix}\right.\)
Phương trình trung trực \(d_1\) của MN vuông góc MN và qua P có dạng
\(1\left(x-\dfrac{3}{2}\right)-2\left(y-2\right)=0\Leftrightarrow x-2y+\dfrac{5}{2}=0\)
\(\Rightarrow\) Tọa độ I là nghiệm:
\(\left\{{}\begin{matrix}3x+7y+1=0\\x-2y+\dfrac{5}{2}=0\end{matrix}\right.\) \(\Rightarrow I\left(-\dfrac{3}{2};\dfrac{1}{2}\right)\)
\(\Rightarrow R^2=IM^2=\left(2+\dfrac{3}{2}\right)^2+\left(1-\dfrac{1}{2}\right)^2=\dfrac{25}{2}\)
Phương trình:
\(\left(x+\dfrac{3}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\dfrac{25}{2}\)