Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(I\) là tâm nằm trên đường trung trực \(OA\)
\(\Rightarrow IA=d\left(I,d\right)\Leftrightarrow\sqrt{\left(x_0+1\right)^2+x^2_0}=\dfrac{\left|-x_0+x_0+1-1\right|}{\sqrt{2}}\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-1\end{matrix}\right.\)
Khi đó: \(\left\{{}\begin{matrix}x_0=0\Rightarrow r=1\\x_0=-1\Rightarrow r=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2+\left(y-1\right)^2=1\\\left(x+1\right)^2+y^2=1\end{matrix}\right.\)

1.
Gọi \(I\left(x;y\right)\) là tâm đường tròn \(\Rightarrow\overrightarrow{AI}=\left(x-1;y-3\right)\)
Do đường tròn tiếp xúc với \(d_1;d_2\) nên:
\(d\left(I;d_1\right)=d\left(I;d_2\right)\Rightarrow\dfrac{\left|5x+y-3\right|}{\sqrt{26}}=\dfrac{\left|2x-7y+1\right|}{\sqrt{53}}\)
Chà, đề đúng ko em nhỉ, thế này thì vẫn làm được nhưng rõ ràng nhìn 2 cái mẫu kia thì số liệu sẽ xấu 1 cách vô lý.
2.
Phương trình đường thẳng kia là gì nhỉ? \(2x+y=0\) à?

Gọi tâm của đường tròn là điểm \(I(a;b)\)
Ta có: \(IA = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} ,d\left( {I,Ox} \right) = b,d\left( {I,Oy} \right) = a\)
Giải hệ phương trình \(\left\{ \begin{array}{l}d\left( {I,Ox} \right) = IA\\d\left( {I,Oy} \right) = IA\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} \\a = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} \end{array} \right.\)
Thay \(a = b\) vào phương trình \(a = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {b - 2} \right)}^2}} \) ta có:
\(\begin{array}{l}a = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {a - 2} \right)}^2}} \\ \Rightarrow {a^2} = {\left( {a - 4} \right)^2} + {\left( {a - 2} \right)^2}\\ \Rightarrow {a^2} - 12a + 20 = 0\\ \Rightarrow \left[ \begin{array}{l}a = 10\\a = 2\end{array} \right. \end{array}\)
Với \(a = b = 2\) ta có phương trình đường tròn (C) là: \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\)
Với \(a = b = 10\) ta có phương trình đường tròn (C) là: \({\left( {x - 10} \right)^2} + {\left( {y - 10} \right)^2} = 100\)

Đáp án D
Đặt f( x; y) = 2x – y+ 4.
Ta có: f( 1; 3) = 3> 0 và f( -2; 5) = -4 – 5+ 4= -5 <0
=> A và B nằm ở 2 phía so với đường thẳng d.
=> không có đường tròn nào thỏa mãn đầu bài.

a) (C) có tâm I và đi qua M nên bán kính R = IM
Ta có: 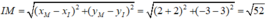
Vậy đường tròn (C) : (x + 2)2 + (y – 3)2 = 52.
b) (C) tiếp xúc với (Δ) : x – 2y + 7 = 0
⇒ d(I; Δ) = R
Mà 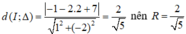
Vậy đường tròn (C) : 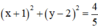
c) (C) có đường kính AB nên (C) có :
+ tâm I là trung điểm của AB
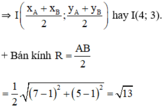
Vậy đường tròn (C) : (x – 4)2 + (y – 3)2 = 13.

a) Gọi đường tròn cần tìm là \(\left(C\right):x^2+y^2-2ax-2by+c=0\)
\(A\left(-1;1\right)\in\left(C\right)\Rightarrow1+1+2a-2b+c=0\Rightarrow2a-2b+c=-2\)
\(B\left(3;1\right)\in\left(C\right)\Rightarrow9+1-6a-2b+c=0\Rightarrow-6a-2b+c=-10\)
\(C\left(1;3\right)\in\left(C\right)\Rightarrow1+9-2a-6b+c=0\Rightarrow-2a-6b+c=-10\)
Giải hệ phương trình ta được: \(a=1;b=1;c=-2\)
Vậy đường tròn cần tìm là: \(x^2+y^2-2x-2y-2=0\)
b) Ta có \(\left(C\right):x^2+y^2-4x+6y+3=0\)
\(\Rightarrow a=\dfrac{-4}{-2}=2;b=\dfrac{6}{-2}=-3;c=3\)
\(\Rightarrow I\left(2;-3\right)\) là tâm, bán kính \(R=\sqrt{2^2+\left(-3\right)^2-3}=\sqrt{10}\)
Để \(\left(\Delta\right)\) tiếp xúc đường tròn \(\Leftrightarrow d\left(I;\Delta\right)=R\)
\(\Leftrightarrow\dfrac{\left|9+m\right|}{\sqrt{10}}=\sqrt{10}\Leftrightarrow\left|9+m\right|=10\Leftrightarrow\left[{}\begin{matrix}9+m=10\\9+m=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-19\end{matrix}\right.\)

