Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: \(=2x^2-3xy+5y^2\)
b: \(=\dfrac{2x^3-10x^2-11x^2+55x+12x-60}{x-5}=2x^2-11x+12\)
c: \(=\dfrac{6x^3+3x^2-10x^2-5x+4x+2}{2x+1}=3x^2-5x+2\)
c: \(=\dfrac{\left(x+3\right)^2-y^2}{x+y+3}=x+3-y\)

a) (x + 2) . (x + 3) - (x - 2) . (x + 5) = 6
=> (x . x + 3x + 2x + 2 . 3) - (x . x + 5x - 2x - 2 . 5) = 6
=> (x2 + 5x + 6) - (x2 + 3x - 10) = 6
=> x2 + 5x + 6 - x2 - 3x + 10 = 6
=> 2x +16 = 6 => 2x = -10 => x = -5
b) (3x + 2) . (2x + 9) - (x + 2) . (6x + 1) = (x + 1) - (x - 6)
=> (3x . 2x + 3x . 9 + 2 . 2x + 2 . 9) - (x . 6x + 1x + 2 . 6x + 2 .1) = x + 1 - x + 6
=> (6x2 + 31x + 18) - (6x2 + 13x + 2) = 7
=> 6x2 + 31x + 18 - 6x2 - 13x - 2 = 7
=> 18x + 16 = 7 => 18x = 9 => x = 0,5
c) 3 . (2x - 1) . (3x - 1) - (2x - 3) . (9x - 1) = 0
=> 3(2x . 3x - 2x -3x + 1) - (2x . 9x - 2x -3 . 9x + 3) = 0
=> 3(6x2 - 5x +1) - (18x2 - 29x + 3) = 0
=> (18x2 -15x + 1) -(18x2 - 29x +3) = 0
=> 18x2 - 15x +1 -18x2 + 29x - 3 = 0
=> 14x = 0 => x = 0

a)(x+2)(x+3)-(x-2)(x+5)=6
x(x+3)+2(x+3)-x(x+5)+2(x+5)=6
x2+3x+2x+6-x2-5x+2x+10=6
(x2-x2)+(3x+2x-5x+2x)+(10+6)=6
2x+16=6
2x=6-16
2x=-10
x=-10/2
x=-5. Vậy x=-5
b)3x(2x+9)+2(2x+9)-x(6x+1)-2(6x+1)=x+1-x+6
6x2+27x+4x+18-6x2-x-12x-2=7
(6x2-6x2)+(27x+4x-x-12x)+(18-2)=7
18x+16=7
18x=7-16
x=-9/18=-1/2. Vậy x=-1/2
c)[3(3x-1)](2x-1)-(2x-3)(9x-1)=0
(9x-3)(2x-1)-(2x-3)(9x-1)=0
9x(2x-1)-3(2x-1)-2x(9x-1)+3(9x-1)=0
18x2-9x-6x+3-18x2+2x+27x-3=0
(18x2-18x2)+(27x+2x-6x-9x)+(3-3)=0
14x=0
x=0/14
x=0. Vậy x=0
a) (x + 2) . (x + 3) - (x - 2) . (x + 5) = 6 => (x . x + 3x + 2x + 2 . 3) - (x . x + 5x - 2x - 2 . 5) = 6
=> (x2 + 5x + 6) - (x2 + 3x - 10) = 6
=> x2 + 5x + 6 - x2 - 3x + 10 = 6
=> 2x +16 = 6 => 2x = -10 => x = -5
b) (3x + 2) . (2x + 9) - (x + 2) . (6x + 1) = (x + 1) - (x - 6)
=> (3x . 2x + 3x . 9 + 2 . 2x + 2 . 9) - (x . 6x + 1x + 2 . 6x + 2 .1) = x + 1 - x + 6
=> (6x2 + 31x + 18) - (6x2 + 13x + 2) = 7
=> 6x2 + 31x + 18 - 6x2 - 13x - 2 = 7
=> 18x + 16 = 7 => 18x = -9 => x = -0,5
c) 3 . (2x - 1) . (3x - 1) - (2x - 3) . (9x - 1) = 0
=> 3(2x . 3x - 2x - 3x + 1) - (2x . 9x - 2x - 3. 9x + 3) = 0
=> 3(6x2 - 5x + 1) - (18x2 - 29x + 3) = 0
=> 18x2 - 15x + 3 - 18x2 + 29x -3 = 0
=> 14x = 0 => x = 0.

1/ \(2x^2+3x-5=\left(2x^2+2x\right)-\left(5x+5\right)=2x\left(x+1\right)-5\left(x+1\right)=\left(x+1\right)\left(2x-5\right)\)
2/ \(16x-5x^2-3=\left(15x-5x^2\right)+\left(x-3\right)=5x\left(3-x\right)-\left(3-x\right)=\left(3-x\right)\left(5x-1\right)\)
3/ \(7x-6x^2-2=\left(3x-6x^2\right)-\left(2-4x\right)=3x\left(1-2x\right)-2\left(1-2x\right)=\left(1-2x\right)\left(3x-2\right)\)
4/ \(x^2+5x-6=\left(x^2-x\right)+\left(6x-6\right)=x\left(x-1\right)+6\left(x-1\right)=\left(x-1\right)\left(x+6\right)\)

Cách 1: Thực hiện phép chia
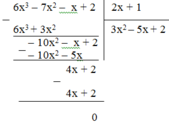
Vậy (6x3 – 7x2 – x + 2) : (2x + 1) = 3x2 – 5x + 2
Cách 2: Phân tích 6x3 – 7x2 – x + 2 thành (2x + 1).P(x) + R(x)
6x3 – 7x2 – x + 2
= 6x3 + 3x2 – 10x2 – 5x + 4x + 2
(Tách -7x2 = 3x2 – 10x2; -x = -5x + 4x)
= 3x2.(2x + 1) – 5x.(2x + 1) + 2.(2x + 1)
= (3x2 – 5x + 2)(2x + 1)
Vậy (6x3 – 7x2 – x + 2) : (2x + 1) = 3x2 – 5x + 2
Giải thích cách tách:
Vì có 6x3 nên ta cần thêm 3x2 để có thể phân tích thành 3x2(2x + 1). Do đó ta tách -7x2 = 3x2 – 10x2.
Lại có -10x2 nên ta cần thêm -5x để có thể phân tích thành -5x(2x + 1). Do đó ta tách –x = -5x + 4x.
Có 4x, ta cần thêm 2 để có 2.(2x + 1) nên 2 không cần phải tách.

a) (x - 1) . (x5 + x4 + x3 + x2 + x + 1) = (x . x5 + x . x4 + x . x3 + x . x2 + x . x + x . 1) - (1 . x5 + 1 . x4 + 1 . x3 + 1 . x2 + 1 . x + 1 . 1)
= (x6 + x5 + x4 + x3 + x2 + x ) - (x5 + x4 + x3 + x2 + x + 1)
= x6 + x5 + x4 + x3 + x2 + x - x5 - x4 - x3 - x2 - x - 1
= x6 + (x5 - x5) + (x4 - x4) + (x3 - x3) + (x2 - x2) + (x - x) - 1
= x6 - 1
b) (x + 1) . (x6 - x5 + x4 - x3 + x2 - x + 1) = (x . x6 - x . x5 + x . x4 - x . x3 + x . x2 - x . x + x . 1) + (1 . x6 - 1 . x5 + 1 . x4 - 1 . x3 + 1 . x2 - 1 . x + 1 . 1)
= (x7 - x6 + x5 - x4 + x3 - x2 + x ) + (x6 - x5 + x4 - x3 + x2 - x + 1)
= x7 - x6 + x5 - x4 + x3 - x2 + x + x6 - x5 + x4 - x3 + x2 - x + 1
= x7+(-x6 + x6) + (x5 - x5) + (-x4 + x4) + (x3 - x3) + (-x2 + x2) + (x - x) + 1
= x7 + 1

1/ \(x^2+x-90=\left(x^2-10x\right)+\left(9x-90\right)=x\left(x-10\right)+9\left(x-10\right)=\left(x-10\right)\left(x+9\right)\)
2/ \(2x^2+4xy+2y^2=\left(2x^2+2xy\right)+\left(2xy+2y^2\right)=2x\left(x+y\right)+2y\left(x+y\right)=\left(x+y\right)\left(2x+2y\right)\)
3/ \(2y^2-14y+24=2\left(y^2-7y+12\right)=2\left[\left(y^2-4y\right)+\left(12-3y\right)\right]=2\left[y\left(y-4\right)-3\left(y-4\right)\right]\)
\(=2\left(y-4\right)\left(y-3\right)\)
4/ \(x^8+x^4+1=\left(x^8+x^7+x^6\right)-\left(x^7+x^6+x^5\right)+\left(x^5+x^4+x^3\right)-\left(x^3+x^2+x\right)+\left(x^2+x+1\right)\)
\(=x^6\left(x^2+x+1\right)-x^5\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^6-x^5+x^3-x+1\right)\)
\(=\left(x^2+x+1\right)\left[\left(x^6-x^5+x^4\right)-\left(x^4-x^3+x^2\right)+\left(x^2-x+1\right)\right]\)
\(=\left(x^2+x+1\right)\left[x^4\left(x^2-x+1\right)\right]-x^2\left(x^2-x+1\right)+\left(x^2-x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4-x^2+1\right)\)

\(a,=\left(6x^3+3x^2-10x^2-5x+4x+2\right):\left(2x+1\right)\\ =\left(2x+1\right)\left(3x^2-5x+2\right):\left(2x+1\right)=3x^2-5x+2\\ b,=\left(x^4-2x^3+3x^2+x^3-2x^2+3x\right):\left(x^2-2x+3\right)\\ =\left(x^2-2x+3\right)\left(x^2+x\right):\left(x^2-2x+3\right)=x^2+x\)
\(\left(6x^3-7x^2-x+2\right):\left(2x+1\right)\)
\(=\left(x+\frac{1}{2}\right)\left(x-1\right)\left(x-\frac{2}{3}\right):\left(x+\frac{1}{2}\right)\)
\(=\left(x-1\right)\left(x-\frac{2}{3}\right)\)
a) Ta có: 6x^3 - 7x2 - x+2 = 6x3+3x2-10x2-5x+4x+2
= 3x2 ( 2x+1) - 5x(2x+1) + 2(2x+1)
= (2x+1)(3x2-5x+2)
Suy ra: (6x3-7x2-x+2): (2x+1)= 3x2-5x+2
b) Ta có: x2 -y2+6x+9= (x2+6x+9) - y2
= (x+3)2 - y2
= (x+3-y)(x+3+y)
Suy ra: (x2-y2+6x+9): (x+y+3)= x-y+3
Làm vậy nha pạn :)