Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{-6}{30}=\frac{x}{-20}\)
nhân chéo \(x\cdot30=\left(-6\right)\cdot\left(-20\right)\)
=>\(30x=120\)
\(x=4\)
\(\frac{-6}{30}=\frac{3}{y}\)
nhân chéo => \(-6x=90\)
\(x=-15\)
\(\frac{-6}{30}=\frac{z}{5}\)
nhân chéo => \(30z=-30\)
\(z=-1\)
x/-20 = -6/30
=> 30x = 120
<=> x = 4
3/y = -6/30
=> -6y = 90
<=> y = -15
z/5 = -6/30
=> -6z = 150
<=> z = - 25

10 + (2x - 1) 2 : 3 = 13
=> (2x - 1) 2 : 3 = 13 - 10
=> (2x - 1) 2 : 3 = 3
=> (2x - 1) 2 = 3 . 3
=> (2x - 1) 2 = 3 2
=> 2x - 1 = 3
=> 2x = 3 + 1
=> 2x = 4
=> x = 2
10 + (2x - 1)2 : 3 = 13
=> (2x - 1)2 : 3 = 13 - 10
=> (2x - 1 )2 : 3 = 3
=> (2x - 1)2 = 9
=> (2x - 1)2 = 32
=> 2x - 1 = 3
=> 2x = 4
=> x = 2
Vậy x = 2

\(\Leftrightarrow164-4\left(x-5\right)=80\\ \Leftrightarrow4\left(x-5\right)=84\\ \Leftrightarrow x-5=21\Leftrightarrow x=26\)

1.
$(a+b+c)-(a-b+c)=a+b+c-a+b-c=(a-a)+(b+b)+(c-c)=0+2b+0=2b$
2.
$(a-b+c)-(a-b+c)=0$
3.
$(a+b+c)-(b-a+c)=a+b+c-b+a-c=(a+a)+(b-b)+(c-c)=2a+0+0=2a$
4.
$(a-c)-(d+b+a+c)=a-c-d-b-a-c=(a-a)+(-c-c)-d-b=0-2c-d-b=-2c-d-b$
5.
$(a+d-c)-(a+b-c)=a+d-c-a-b+c=(a-a)+(-c+c)+d-b=0+0+d-b=d-b$
6.
$(a-b+c+d)+(a+c-d-b)=a-b+c+d+a+c-d-b$
$=(a+a)+(-b-b)+(c+c)+(d-d)=2a-2b+2c$
7.
$(a+d-c)+(a-b+c)=a+d-c+a-b+c=(a+a)+d+(-c+c)=2a+d$

a, => x^3 < 0 ; x-3 > 0 hoặc x^3 > 0 ; x-3 < 0
=> 0 < x < 3
b, => x^4.(2x-8) < 0
=> x^4.(x-4) < 0
Vì x^4 >= 0
=> x-4 < 0
=> x < 4
c, Vì x-1 < x+12
=> x-1 < 0 ; x+12 >0
=> -12 < x < 1
d, => x-12 > 0 ; x-1 > 0 hoặc x-12 < 0 ; x-1 < 0
=> x >12 hoặc x < 1
Tk mk nha


\(x.y+2y+x=6\)
\(\Rightarrow y.\left(x+2\right)+\left(x+2\right)-2=6\)
\(\Rightarrow y.\left(x+2\right)+\left(x+2\right)=8\)
\(\Rightarrow\left(x+2\right).\left(y+1\right)=8\)
\(\Rightarrow\left(x+2\right).\left(y+1\right)\inƯ\left(8\right)=\left\{1;2;4;8\right\}\) mà : \(x+2\ge2\)
\(\Rightarrow\) \(x+2=2\Rightarrow x=0\)
\(y+1=4\Rightarrow y=3\)
\(\Rightarrow x=0;y=3\)

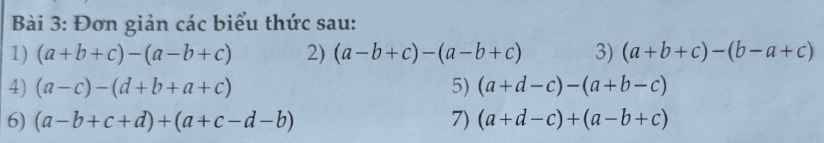
Vì /x/ >hoặc=0 mà /x/+x=6 suy ra x>hoặc=0
/x/+x=6
suy ra: x+x=6
suy ra: 2x=6
suy ra: x=6:2
suy ra: x=3
Vậy x =3
Chúc bạn học tốt....
Th1:\(x\le0\)
\(\Rightarrow|x|=-x\)
Khi đó ta có:\(|x|+x=\left(-x\right)+x=0=6\)(loại)
Th2:x>0
\(\Rightarrow|x|=x\)
Khi đó ta có:\(|x|+x=x+x=2x=6\Rightarrow x=3\)(Thỏa mãn)
Vậy x=3