K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
18 tháng 7 2021
Gọi số sản phẩm àm 2 ng công nhân được giao là x (x∈N*, sản phẩm)
Thời gian hoàn thành công việc của người thứ nhất là: \(\dfrac{x}{40}\left(h\right)\)
Thời gian hoàn thành công việc của ngươi thứ hai là: \(\dfrac{x}{50}\left(h\right)\)
Vì ng thứ nhất hoàn thành công việc chậm hơn người thứ hai 2 giờ nên ta có PT:
\(\dfrac{x}{40}-\dfrac{x}{50}=2\)
⇔\(50x-40x=4000\)
⇔\(10x=4000\)
⇔\(x=400\)
Vậy số sản phẩm mỗi công nhân được giao là 400 (sản phẩm)
TH
Giúp em với ạ
0
làm hộ em bài 2 với ạ
13 tháng 7 2021
1)
a) 4y2-4xy+x2= x2-4xy+4y2= (x-2y)2
b) 9x2-12xy+4y2= (3x)2-2.3x.2y+(2y)2= (3x-2y)2
c) 16x2-25=(4x)2-52= (4x-5)(4x+5)
d) 1-9y2= 12-(3y)2=(1-3y)(1+3y)
13 tháng 7 2021
g) x3-27y3= (x-3y)(x2+3xy+9y2)
h) 64 + 8x3=(4+2x)(16+8x+4x2)
2 tháng 12 2021
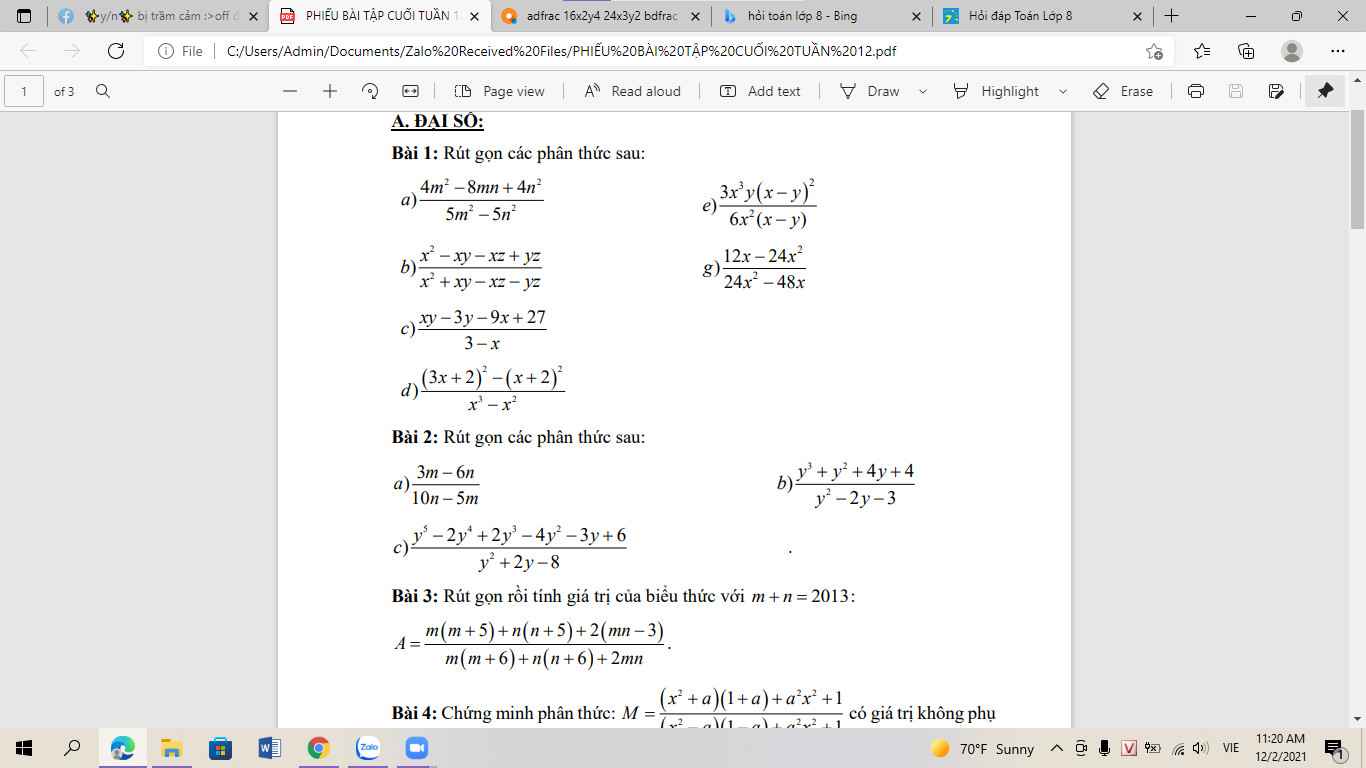
Bài 1:
a) \(=\dfrac{\left(2m-2n\right)^2}{5\left(m^2-n^2\right)}=\dfrac{4\left(m-n\right)^2}{5\left(m-n\right)\left(m+n\right)}=\dfrac{4m-4n}{4m+5n}\)
b) \(=\dfrac{\left(x-y\right)\left(x-z\right)}{\left(x+y\right)\left(x-z\right)}=\dfrac{x-y}{x+y}\)
c) \(=\dfrac{\left(x-3\right)\left(y-9\right)}{-\left(x-3\right)}=9-y\)
d) \(=\dfrac{\left(3x+2-x-2\right)\left(3x+2+x+2\right)}{x^2\left(x-1\right)}=\dfrac{8x\left(x+1\right)}{x^2\left(x-1\right)}=\dfrac{8x+8}{x^2-x}\)
e) \(=\dfrac{xy\left(x-y\right)}{2}=\dfrac{x^2y-xy^2}{2}\)
g) \(=\dfrac{12x\left(1-2x\right)}{24x\left(x-2\right)}=\dfrac{1-2x}{2x-4}\)
Bài 2:
a) \(=\dfrac{3\left(m-2n\right)}{-5\left(m-2n\right)}=-\dfrac{3}{5}\)
b) \(=\dfrac{\left(y+1\right)\left(y^2+4\right)}{\left(y-3\right)\left(y+1\right)}=\dfrac{y^2+4}{y-3}\)
c) \(=\dfrac{y^4\left(y-2\right)+2y^2\left(y-2\right)-3\left(y-2\right)}{\left(y-2\right)\left(y+4\right)}=\dfrac{\left(y-2\right)\left(y^4+2y^2-3\right)}{\left(y-2\right)\left(y+4\right)}=\dfrac{y^4+2y^2-3}{y+4}\)
Bài 3:
\(A=\dfrac{\left(m^2+2mn+n^2\right)+5\left(m+n\right)-6}{\left(m^2+2mn+n^2\right)+6\left(m+n\right)}=\dfrac{\left(m+n\right)^2+5\left(m+n\right)-6}{\left(m+n\right)^2+6\left(m+n\right)}=\dfrac{2013^2+5.2013-6}{2013^2+6.2013}=\dfrac{2012}{2013}\)
YN
2 tháng 5 2022
\(\left(x-1\right)^3+x^3+\left(x+1\right)^3=\left(x+2\right)^3\)
\(\Leftrightarrow x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1-x^3-6x^2-12x-8=0\)
\(\Leftrightarrow2x^3-6x^2-6x-8=0\)
\(\Leftrightarrow2.\left(x^3-3x^2-3x-4\right)=0\)
\(\Leftrightarrow x^3-4x^2+x^2-4x+x-4=0\)
\(\Leftrightarrow x^2.\left(x-4\right)+x.\left(x-4\right)+\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right).\left(x^2+x+1\right)=0\)
Mà \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
\(\Rightarrow x-4=0\Leftrightarrow x=4\)
24 tháng 3 2021
Câu 3:
Gọi độ dài quãng đường AB là x(km)
Thời gian xe máy đi từ A đến B là: \(\dfrac{x}{30}\left(h\right)\)
Thời gian xe máy đi từ B về A là: \(\dfrac{x}{35}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{x}{30}+\dfrac{x}{35}=\dfrac{13}{3}\)
\(\Leftrightarrow\dfrac{7x}{210}+\dfrac{6x}{210}=\dfrac{910}{210}\)
\(\Leftrightarrow13x=910\)
hay x=70(thỏa ĐK)
Vậy: Độ dài quãng đường AB là 70km
3 tháng 3 2021
Câu 1:
a) Xét ΔABC có
M\(\in\)AB(gt)
N\(\in\)AC(gt)
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(=\dfrac{1}{3}\right)\)
Do đó: MN//BC(Định lí Ta lét đảo)
HN
3 tháng 3 2021
Câu 1:
a) Xét \(\Delta ABC\) có:
\(\left\{{}\begin{matrix}\dfrac{AM}{AB}=\dfrac{2}{6}=\dfrac{1}{3}\\\dfrac{AN}{AC}=\dfrac{3}{9}=\dfrac{1}{3}\end{matrix}\right.\)
⇒ \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(=\dfrac{1}{3}\right)\)
⇒ MN // BC (Theo định lí Ta-lét đảo) \(\left(ĐPCM\right)\)
b)
Xét \(\Delta ABC\) có MN//BC (cmt)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MN}{BC}\) ⇒ \(\dfrac{AM}{MN}=\dfrac{AB}{BC}\) \(\left(1\right)\)
Xét \(\Delta ABC\) có NK//AB (gt)
⇒ \(\dfrac{AB}{NK}=\dfrac{BC}{CK}\) ⇒ \(\dfrac{AB}{BC}=\dfrac{NK}{CK}\) (2)
Từ (1) và (2) ⇒ \(\dfrac{AM}{MN}=\dfrac{NK}{CK}\)
⇒ \(AM.KC=NK.MN\) \(\left(ĐPCM\right)\)
Bài 1:
a: =8xy/2x=4y
b: \(=\dfrac{4x-1-7x+1}{3x^2y}=\dfrac{-3x}{3x^2y}=\dfrac{-1}{xy}\)
c: \(=\dfrac{3x-x+6}{2x\left(x+3\right)}=\dfrac{2\left(x+3\right)}{2x\left(x+3\right)}=\dfrac{1}{x}\)
e: \(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}=\dfrac{-10}{4}=-\dfrac{5}{2}\)
câu 3 bài 1: = (x-y)(y-1)