
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 2:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\begin{cases}a=kb\\c=kd\end{cases}\)
=> \(\frac{5a+3b}{5a-3b}=\frac{5kb+3b}{5kb-3b}=\frac{b\left(5k+3\right)}{b\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(1\right)\)
\(\frac{5c+3d}{5c-3d}=\frac{5kd+3d}{5kd-3d}=\frac{d\left(5k+3\right)}{d\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(2\right)\)
Từ (1) và (2) => \(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)
Bài 3:
Đặt \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=k^3\)
=> \(\frac{a}{d}=k^3\) (1)
Lại có: \(\frac{a+b+c}{b+c+d}=\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\left(\frac{a+b+c}{b+c+d}\right)^3=k^3\) (2)
Từ (1) và (2) => \(\frac{a}{d}=\left(\frac{a+b+c}{b+c+d}\right)^3\)

\(1,M=\left(\dfrac{\dfrac{2}{5}-\dfrac{2}{9}+\dfrac{2}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}-\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{6}-\dfrac{7}{8}+\dfrac{7}{10}}\right)\cdot\dfrac{2013}{2012}\\ M=\left(\dfrac{2\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}-\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{2}\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}\right)}\right)\cdot\dfrac{2013}{2012}\\ M=\left(\dfrac{2}{7}-\dfrac{2}{7}\right)\cdot\dfrac{2013}{2012}=0\)
\(\left|x^2+\left|x-2\right|\right|=x^2+2021\\ \Leftrightarrow\left[{}\begin{matrix}x^2+\left|x-2\right|=x^2+2021\\x^2+\left|x-2\right|=-x^2-2021\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left|x-2\right|=2021\\\left|x-2\right|=-2x^2-2021\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x-2=\pm2021\\x\in\varnothing\left(-2x^2-2021< 0\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2023\\x=-2019\end{matrix}\right.\)
\(3,\\ A=\left(x-\dfrac{2}{5}\right)^2+\left(y+20\right)^{10}+2022\ge2022\\ A_{min}=2022\Leftrightarrow\left\{{}\begin{matrix}x-\dfrac{2}{5}=0\\y+20=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{5}\\y=-20\end{matrix}\right.\)



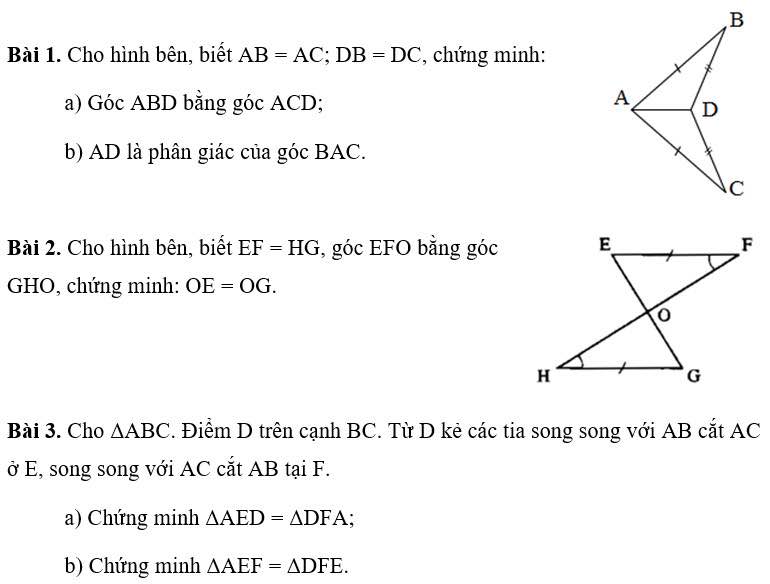
Bài 1 :
a,Có \(AD\) chung , mà \(AB=AC;DB=DC\)
\(\Rightarrow\Delta ABC=\Delta ADC\)
Do đó \(\widehat{ABD}=\widehat{ACD}\)
b,\(AD\) là cạnh chung của 2\(\Delta:\Delta ABD,\Delta ACD\)
\(\Rightarrow AD\) là phân giác của \(\widehat{BAC}\)
Bài 2:
Ta có : \(EF=HG,\widehat{EFO}=\widehat{GHO}\)
Theo TH thứ 2 của 2 tam giác bằng nhau ta có : cạnh - góc - cạnh
\(\Rightarrow OE=OG\)
Bài 3: Có hình ko bn ,mk dựa vào hình lm ko mk lười vẽ hình lắm =(((((((

Biết d song2 với d' thì => góc A1 = góc B3 và:
b) góc A1 = góc B4 và
c) góc A1+ B2=180 độ
a) Nếu 1 đường thẳng cắt 2 đường thẳng song2 thì:
a) 2 góc so le trong bằng nhau
b) 2 góc đồng vị bằng nhau
c) 2 góc trong cùng phía bù nhau
Biết : (hình 25b)
a) góc A4 = góc B2
hoặc b) góc A1 = góc B1
hoặc c) góc A1 + B2 = 180 độ
thì suy ra d song2 với d'
Nếu 1 đường thẳng cắt 2 đường thẳng
mà a) 2 góc so le trong bằng nhau
hoặc b) 2 góc đồng vị bằng nhau
hoặc c) 2 góc trong cùng phía bù nhau thì 2 đường thẳng đó song2 với nhau.
![]()
![]()
![]()
 mình bài 9,10,11 nhé các bạn thân yêu
mình bài 9,10,11 nhé các bạn thân yêu


 Các bạn giúp mình làm bài này gấp nhé!
Các bạn giúp mình làm bài này gấp nhé!
 Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi
Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi
Bài 9:
a) Gọi 3 phần cần tìm lần lượt là a,b,c
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}\) = \(\frac{b}{3}\) = \(\frac{c}{5}\) = \(\frac{a+b+c}{2+3+5}\) = \(\frac{6200}{10}\) = 620
\(\Rightarrow\) \(\left[\begin{array}{nghiempt}a=620.2\\b=620.3\\c=620.5\end{array}\right.\) \(\Rightarrow\) \(\left[\begin{array}{nghiempt}a=1240\\b=1860\\c=3100\end{array}\right.\)
Vậy 3 phần cần tìm lần lượt là 1240 ; 1860 ; 3100
b) Gọi 3 phần cần tìm lần lượt là a, b,c
Vì a , b ,c tỉ lệ nghịch với 2 ; 3 ; 5 nên ta có:
a . 2 = b . 3 = c . 5 và a + b + c = 6200
Có: \(\frac{a}{\frac{1}{2}}\) = \(\frac{b}{\frac{1}{3}}\) = \(\frac{c}{\frac{1}{5}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{\frac{1}{2}}\) = \(\frac{b}{\frac{1}{3}}\) = \(\frac{c}{\frac{1}{5}}\) = \(\frac{a+b+c}{\frac{1}{2}+\frac{1}{3}+\frac{1}{5}}\) = \(\frac{6200}{\frac{31}{30}}\) = 6200 . \(\frac{30}{31}\) = 6000
\(\Rightarrow\) \(\left[\begin{array}{nghiempt}a=6000.\frac{1}{2}\\b=6000.\frac{1}{3}\\c=6000.\frac{1}{5}\end{array}\right.\) \(\Rightarrow\) \(\left[\begin{array}{nghiempt}a=3000\\b=2000\\c=1200\end{array}\right.\)
Vậy 3 phần cần tìm lần lượt là 3000 ; 2000 ; 1200
Bài 10.
a) Vì y tỉ lệ tuận với x nên ta có công thức:
y = kx hay 8 = k6
=> k = \(\frac{8}{6}\) = \(\frac{4}{3}\)
Biểu diễn y theo x : y = \(\frac{4}{3}\) . x
b) Khi x = 9 thì y = \(\frac{4}{3}\) . 9 = 12
c) Khi y = - 4:
Ta có: - 4 = \(\frac{4}{3}\) . x
=> x = -4 : \(\frac{4}{3}\) = -4 . \(\frac{-3}{4}\) = -3
Bài 11.
a) Vì x và y tỉ lệ nghịch với nhau nên ta có công thức:
x . y = a hay 4 . (-15) = -60
Biểu diễn y theo x: y = \(\frac{-60}{x}\)
b) Khi x = 6 thì y = \(\frac{-60}{6}\) = -10
Khi x = -12 thì y = \(\frac{-60}{-12}\) = 5
c)
+) Khi y = -2
Ta có công thức: -2 = \(\frac{-60}{x}\)
=> x = \(\frac{-60}{-2}\) = 30
+) Khi y = 30
Tương tự ta có: x = \(\frac{-60}{30}\) = -2