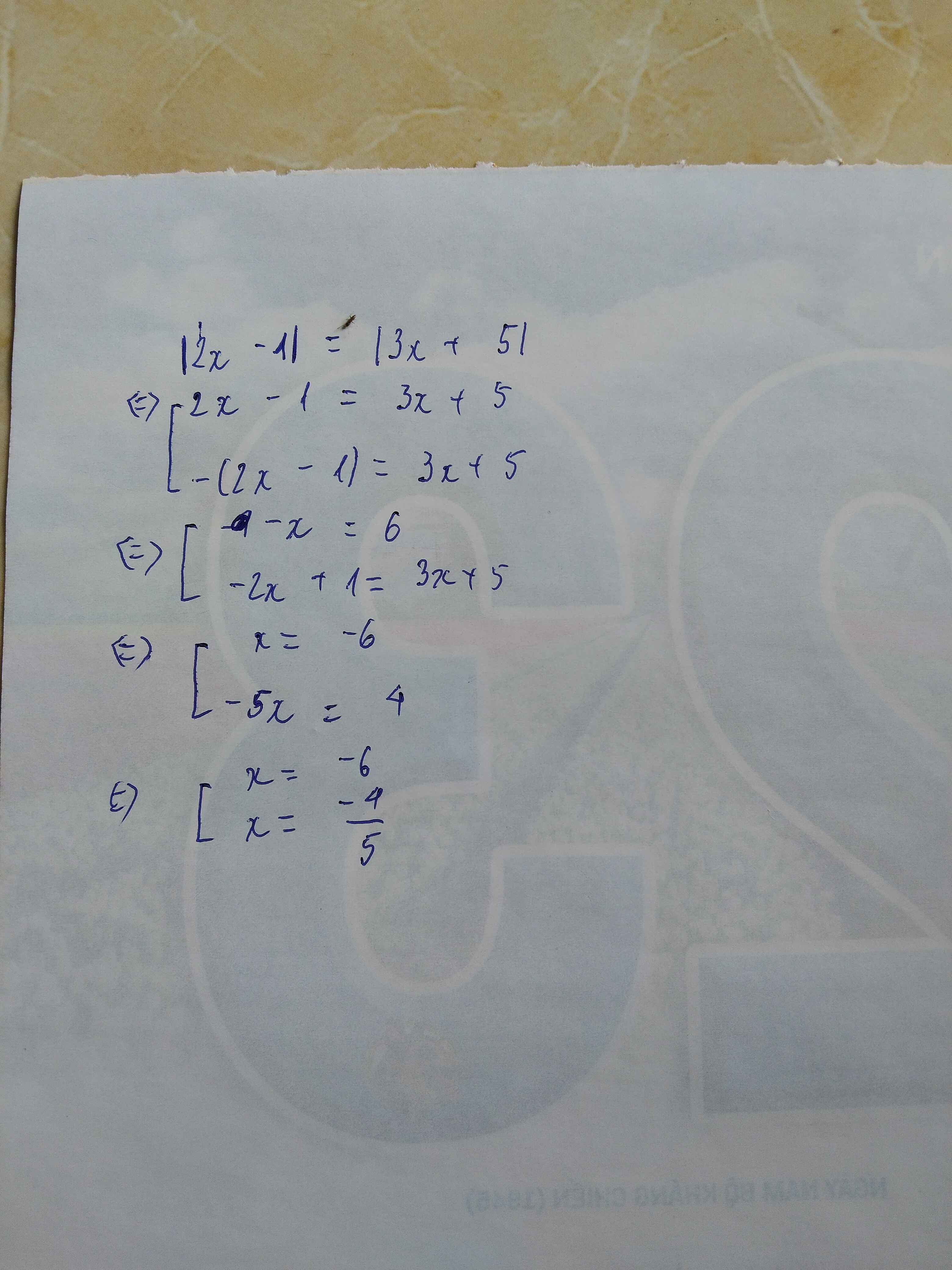Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) |3x-2| + 5x = 4x - 10
<=> |3x-2| = -x - 10
Ta có |3x-2| = 3x-2 nếu x>=2/3 ; = -3x + 2 nếu x<2/3
+TH1: 3x-2 = -x - 10
<=> x = -2 (loại vì x < 2/3)
+TH2: -3x + 2 = -x - 10
<=> x = 6 (loại vì x > 2/3)
Vậy không có x thoả mãn
b) 3 + |2x+5| > 13
<=> |2x+5| > 10
Gợi ý: Xét 2TH: 2x + 5 > 10 và 2x + 5< -10 rồi tìm ra x

\(\left|2x-1\right|=\left|3x+5\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=3x+5\\2x-1=-3x-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-6\\x=-\dfrac{4}{5}\end{matrix}\right.\)

Ta có \(\hept{\begin{cases}\left|3x-5\right|\ge0\forall x\\\left|2x-y\right|\ge0\forall y\end{cases}}\Leftrightarrow\left|3x-5\right|+\left|2x-y\right|\ge0\forall x;y\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}3x-5=0\\2x-y=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{3}\\y=\frac{10}{3}\end{cases}}\)
Vậy x = 5/3 ; y = 10/3 là giá trị cần tìm

Vì \(\hept{\begin{cases}\left|3x-5\right|\ge0\forall x\\\left|2x-y\right|\ge0\forall x,y\end{cases}}\Rightarrow\left|3x-5\right|+\left|2x-y\right|\ge0\forall x,y\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}3x-5=0\\2x-y=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{3}\\y=\frac{10}{3}\end{cases}}\)
Vậy x = 5/3 ; y = 10/3

\(1,|5x|=x-12\)
\(\Rightarrow\orbr{\begin{cases}5x=x-12\\5x=12-x\end{cases}\Rightarrow}\orbr{\begin{cases}4x=-12\\6x=12\end{cases}\Rightarrow\orbr{\begin{cases}x=-3\\x=2\end{cases}}}\)
\(2,|7-x|=5x+1\)
\(\Rightarrow\orbr{\begin{cases}7-x=5x+1\\7-x=-5x-1\end{cases}\Rightarrow}\orbr{\begin{cases}6x=6\\4x=-8\end{cases}\Rightarrow}\orbr{\begin{cases}x=1\\x=-2\end{cases}}\)
\(3,|2x-3|+x=21\)
\(\Rightarrow|2x-3|=21-x\)
\(\Rightarrow\orbr{\begin{cases}2x-3=21-x\\2x-3=x-21\end{cases}\Rightarrow}\orbr{\begin{cases}3x=24\\x=-18\end{cases}\Rightarrow}\orbr{\begin{cases}x=8\\x=-18\end{cases}}\)
\(4,|4+2x|=-4x\)
\(\Rightarrow\orbr{\begin{cases}4+2x=4x\\4+2x=-4x\end{cases}\Rightarrow}\orbr{\begin{cases}2x=4\\-6x=4\end{cases}\Rightarrow}\orbr{\begin{cases}x=2\\x=-\frac{2}{3}\end{cases}}\)
\(5,|3x-1|+2=x\)
\(\Rightarrow|3x-1|=x-2\)
\(\Rightarrow\orbr{\begin{cases}3x-1=x-2\\3x-1=2-x\end{cases}\Rightarrow\orbr{\begin{cases}2x=-1\\4x=3\end{cases}\Rightarrow}\orbr{\begin{cases}x=-\frac{1}{2}\\x=\frac{3}{4}\end{cases}}}\)
\(6,|2x-5|+x=2\)
\(\Rightarrow|2x-5|=2-x\)
\(\Rightarrow\orbr{\begin{cases}2x-5=2-x\\2x-5=x-2\end{cases}\Rightarrow\orbr{\begin{cases}3x=7\\x=3\end{cases}\Rightarrow}\orbr{\begin{cases}x=\frac{7}{3}\\x=3\end{cases}}}\)

-|3x - 7| - |y + 5| - 1 = 0
<=> - 1 = |3x - 7| + |y + 5| (*)
Ta có: VP=|3x - 7| + |y + 5|≥0 với mọi x;y
VT=-1<0
Nên pt (*) vô nghiệm
Vậy pt đã cho vô nghiệm.

(1) : |x-7|=x-7 =>x-7>=0 => x>=7. Vậy (1) đúng với mọi x>=7
(2) : |2x-5| = 5-2x => 5-2x >=0 => 2x<=5 => x<=5/2. Vậy (2) đúng với mọi x<=5/2.
a)\(\left|x-7\right|=x-7\)
\(\Rightarrow\orbr{\begin{cases}x-7=x-7\\x-7=-\left(x-7\right)\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x-x=-7+7\\x-7=-x+7\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}0=0\\x+x=7+7\end{cases}}\)\(\Rightarrow2x=14\)\(\Rightarrow x=14:2=7\)
Vậy \(x=7\)
b) |2x-5|=5-2x
\(\Rightarrow\orbr{\begin{cases}2x-5=2x-5\\2x-5=-\left(5-2x\right)\end{cases}}\Rightarrow\orbr{\begin{cases}2x-2x=-5+5\\2x-5=-5+2x\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}Ox=0\\2x-2x=-5+5\end{cases}}\)
\(\Rightarrow x=0\)