Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

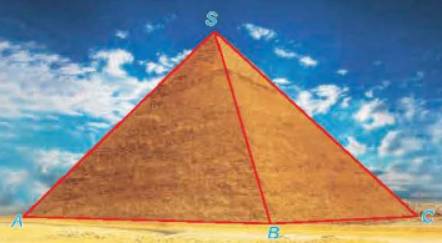
Vì AB // CD (ABCD là hình vuông) nên (SC, AB) = (SC, CD)
Xét tam giác SCD có
\(\cos \widehat {SCD} = \frac{{S{C^2} + C{D^2} - S{D^2}}}{{2SC.CD}} = \frac{{{{219}^2} + {{230}^2} - {{219}^2}}}{{2.219.230}} = \frac{{115}}{{219}} \Rightarrow \widehat {SCD} \approx 58,{32^0}\)
Vậy góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp bằng khoảng 58,320.

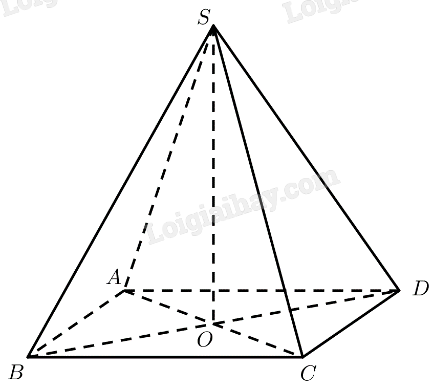
Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\) có \(O\) là tâm của đáy. Kẻ \(SI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right)\).
Ta có: \(SO = 136,CD = 152\)
Tam giác \(SCD\) cân tại \(S\)
\( \Rightarrow SI\) vừa là trung tuyến, vừa là đường cao của tam giác
\( \Rightarrow I\) là trung điểm của \(CD\).
Mà \(O\) là trung điểm của \(AD\)
\( \Rightarrow OI\) là đường trung bình của tam giác \(ACD\)
\( \Rightarrow OI = \frac{1}{2}BC = 76\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI\)
\( \Rightarrow \Delta SOI\) vuông tại \(O\)
\( \Rightarrow SI = \sqrt {S{O^2} + O{I^2}} = 4\sqrt {1517} \approx 155,8\)
Vậy độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp khoảng 155,8 m.

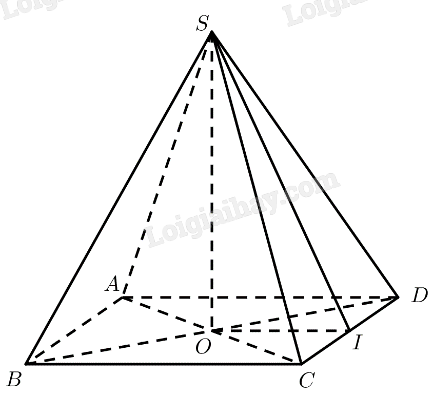
Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\) có \(O\) là tâm của đáy. Kẻ \(SI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right)\).
Ta có: \(SO = 21,6;C{\rm{D}} = 34\)
\(AC = \sqrt {A{B^2} + B{C^2}} = 34\sqrt 2 \Rightarrow OC = \frac{1}{2}AC = 17\sqrt 2 \)
\(\Delta SOC\) vuông tại \(O\)\( \Rightarrow SC = \sqrt {S{O^2} + O{C^2}} \approx 32,3\)
Vậy độ dài cạnh bên bằng \(32,3\left( m \right)\)
Tam giác \(SCD\) cân tại \(S\)
\( \Rightarrow SI\) vừa là trung tuyến, vừa là đường cao của tam giác
\( \Rightarrow I\) là trung điểm của \(CD\).
Mà \(O\) là trung điểm của \(AD\)
\( \Rightarrow OI\) là đường trung bình của tam giác \(ACD\)
\( \Rightarrow OI = \frac{1}{2}BC = 17\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI\)
\( \Rightarrow \Delta SOI\) vuông tại \(O\)\( \Rightarrow SI = \sqrt {S{O^2} + O{I^2}} \approx 27,5\)
\({S_{SC{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.SI \approx 467,5\)
Diện tích xung quanh của kim tự tháp là: \({S_{xq}} = 4{S_{SC{\rm{D}}}} \approx 1870\left( {{m^2}} \right)\)

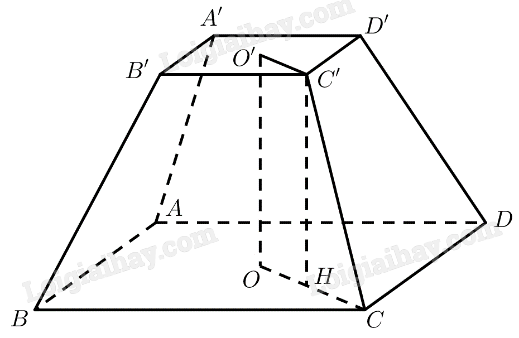
Mô hình hoá chân tháp bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy. Vậy \(AB = 5,A'B' = 2,CC' = 3\).
\(ABCD\) là hình vuông
\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = 5\sqrt 2 \Rightarrow CO = \frac{1}{2}AC = \frac{{5\sqrt 2 }}{2}\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow A'C' = \sqrt {A'B{'^2} + B'C{'^2}} = 2\sqrt 2 \Rightarrow C'O' = \frac{1}{2}A'C' = \sqrt 2 \)
Kẻ \(C'H \bot OC\left( {H \in OC} \right)\)
\(OHC'O'\) là hình chữ nhật \( \Rightarrow OH = O'C' = \sqrt 2 ,OO' = C'H \Rightarrow CH = OC - OH = \frac{{3\sqrt 2 }}{2}\)
\(\Delta CC'H\) vuông tại \(H \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}} = \frac{{3\sqrt 2 }}{2} \Rightarrow OO' = C'H = \frac{{3\sqrt 2 }}{2}\)
Diện tích đáy lớn là: \(S = A{B^2} = {5^2} = 25\left( {{m^2}} \right)\)
Diện tích đáy bé là: \(S' = A'B{'^2} = {2^2} = 4\left( {{m^2}} \right)\)
Thể tích hình chóp cụt là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.\frac{{3\sqrt 2 }}{2}\left( {25 + \sqrt {25.4} + 4} \right) = \frac{{39\sqrt 2 }}{2}\left( {{m^3}} \right)\)
Số tiền để mua bê tông tươi làm chân tháp là: \(\frac{{39\sqrt 2 }}{2}.1470000 \approx 40538432\) (đồng).

THAM KHẢO:

Kẻ SM⊥BC
Mà BC⊥SO nên BC⊥(SOM). Suy ra BC⊥OM
Do đó góc nhị diện tạo bởi mặt bên và mặt đáy là \(\widehat{SMO}\)
Ta có: SO=98;OM=\(\dfrac{1}{2}\).180=90
tan \(\widehat{SMO}\)=\(\dfrac{SO}{OM}\)=1,1. Suy ra \(\widehat{SMO}\)=\(47,4^O\)
Vậy góc nhị diện tạo bởi mặt bên và mặt đáy là \(^{47,4^O}\)
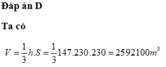


Đáp án D