Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
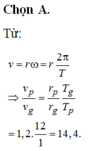
Tốc độ dài của đầu kim phút và kim giờ được tính theo công thức:
Từ đó suy ra
Thay r 1 = 1,5 r 2 ; T 1 = 3600 s; T 2 = 43200 s vào công thức trên ta tìm được
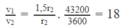
Ta có công thức tính tốc độ dài của kim giờ và kim phút như sau:
\(v_p=\omega r_p=\dfrac{2\pi r_p}{T_p}vav_g=\omega r_g=\dfrac{2\pi r_g}{T_g}\)
\(\Rightarrow\dfrac{v_p}{v_g}=\dfrac{r_p}{r_g}.\dfrac{T_g}{T_p}\)
Thay: \(r_p=1,5r_g;T_p=3600s;T_g=43200s\) vào công thức trên, ta có:
\(\dfrac{v_p}{v_g}=\dfrac{1,5r_g}{r_g}.\dfrac{43200}{3600}18lan\)
Chọn đáp án A
Điểm đầu các kim của đồng hồ chuyển động tròn đều
Gọi ω 1 , ω 2 lần lượt là tốc độ góc của kim phút và kim giờ. Chiều dài của kim phút và kim giờ tương ứng là R 1 , R 2 ta có:
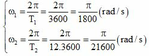
Theo đề bài R 1 = 2 R 2
Tốc độ dài ở điểm đầu kim phút và kim giờ lần lượt là
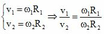
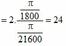
Chu kì quay của kim giờ là \(T_g=12h\); của kim phút là \(T_{ph}=1h\)
Có: \(T_g=\frac{2\pi}{w_g};T_{ph}=\frac{2\pi}{w_{ph}}\)
Ta được tỉ số \(\frac{T_g}{T_{ph}}=\frac{w_{ph}}{w_g}=12\)
Mà \(w_g=\frac{v_g}{R_g};w_{ph}=\frac{v_{ph}}{R_{ph}}\)
Vậy \(\frac{v_{ph}}{v_g}=\frac{w_{ph}}{w_g}\cdot\frac{R_{ph}}{R_g}=12\cdot1,5=18\left(lần\right)\)
