
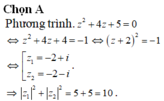
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

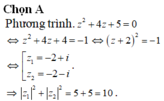

\(\Delta'=4-5=-1\Rightarrow\left[{}\begin{matrix}z_1=2+i\\z_2=2-i\end{matrix}\right.\)
\(\Rightarrow\left(z_1-1\right)^{2019}+\left(z_2-1\right)^{2019}=\left(i+1\right)^{2019}+\left(i-1\right)^{2019}\)
\(=\left(i+1\right)\left[\left(i+1\right)^2\right]^{1009}+\left(i-1\right)\left[\left(i-1\right)^2\right]^{1009}\)
\(=\left(i+1\right)\left(2i\right)^{1009}+\left(1-i\right)\left(-2i\right)^{1009}=\left(2i\right)^{1009}\left(i+1+i-1\right)=\left(2i\right)^{1009}.2i=\left(2i\right)^{1010}=-2^{1010}\)
=>D
P/s: Sry nó bị trôi thông báo nên toi ko để ý

\(z^2-4z+5=0\Rightarrow\left\{{}\begin{matrix}z_1+z_2=4\\z_1z_2=5\end{matrix}\right.\) theo hệ thức Viet
\(w=\dfrac{z_1+z_2}{z_1z_2}+i.z_1z_2\left(z_1+z_2\right)=\dfrac{4}{5}+i.5.4=\dfrac{4}{5}+20i\)

Chắc bạn ghi nhầm đề \(z_1\overline{z_2}+\overline{z_1}z_2\) mới có lý chứ nhỉ?
Khi pt bậc 2 có 2 nghiệm phức \(z_1;z_2\) thì \(z_1=\overline{z_2}\)
Do đó \(z_1\overline{z_2}+\overline{z_1}z_2=z_1^2+z_2^2=\left(z_1+z_2\right)^2-2z_1z_2=\left(-4\right)^2-2.7=2\)

Đặt a + bi(a, b ∈R). Ta có:
( 1 + 2 i ) 2 z = ( 1 + 2 i - 4 ) ( a + b i ) = - 3 a - 3 b i + 4 a i - 4 b = - 3 a - 4 b + ( 4 a - 3 b ) i
Do đó: ( 1 + 2 i ) 2 . z + a = 4 i - 20 <=> -3a - 4b + (4a - 3b)i + a - bi = 4i - 20
<=> -2a - 4b + (4a - 4b)i = 4i - 20
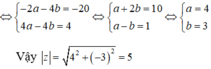
Chọn B