Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



15:
a: \(\text{Δ}=\left(m^2-m+2\right)^2-4m^2\)
=(m^2-m+2-2m)(m^2-m+2+2m)
=(m^2+m+2)(m^2-3m+2)
=(m-1)(m-2)(m^2+m+2)
Để phương trình co hai nghiệm phân biệt thì (m-1)(m-2)(m^2+m+2)>0
=>(m-1)(m-2)>0
=>m>2 hoặc m<1
b: x1+x2=m^2-m+2>0 với mọi m
x1*x2=m^2>0 vơi mọi m
=>Phương trình luôn có hai nghiệm dương phân biệt

a: 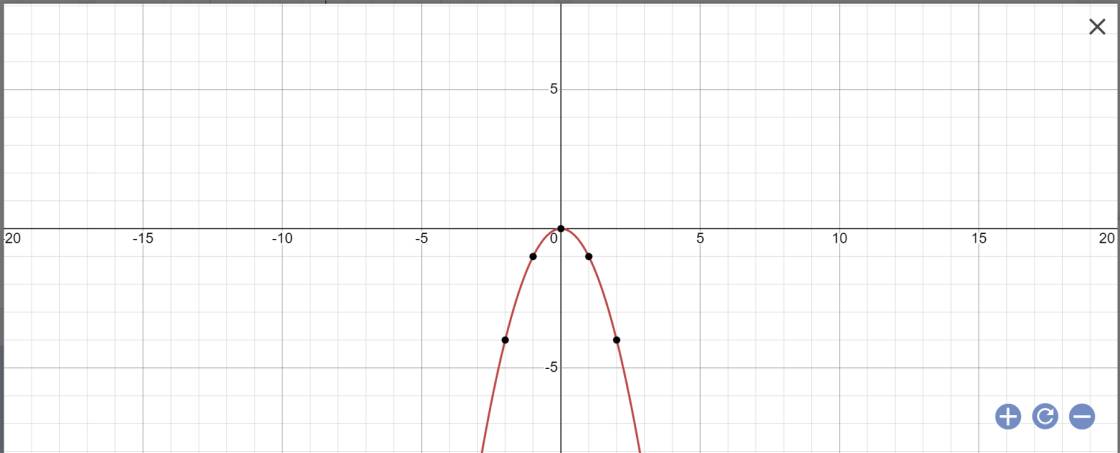
b: PTHĐGĐ là:
-x^2-2x+3m=0
=>x^2+2x-3m=0
Δ=(-2)^2-4*(-3m)=12m+4
Để (P) cắt (d) tại hai điểm pb thì 12m+4>0
=>m>-1/3
Sửa đề: x1.x2^2+x2.(3m-2x1)= 6
<=> x2.( x1.x2+3m-2x1) = 6
<=> x2.( -3m+3m-2x1) = 6
<=> -2x1x2 = 6
<=> x1.x2 =-3
<=> -3m =-3
<=> m=1





a: Xét (O) có
ΔAMB nội tiếp đường tròn
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét tứ giác AMCK có
\(\widehat{AKC}+\widehat{AMC}=180^0\)
nên AMCK là tứ giác nội tiếp
hay A,M,C,K cùng thuộc một đường tròn



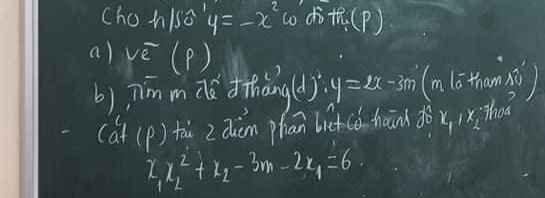





\(A=\dfrac{\sqrt{60}}{\sqrt{15}}=\sqrt{\dfrac{60}{15}}=\sqrt{4}=2\)
\(B=\sqrt{\dfrac{72}{15}}:\sqrt{\dfrac{2}{15}}=\sqrt{\dfrac{72}{15}}\cdot\sqrt{\dfrac{15}{2}}=\sqrt{\dfrac{72}{2}}=\sqrt{36}=6\)
\(C=\left(\sqrt{3}+\sqrt{2}\right)\cdot\left(\sqrt{2}-\sqrt{3}\right)=\left(\sqrt{2}\right)^2-\left(\sqrt{3}\right)^2=2-3=-1\)
cảm ơn ạ