Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Phương pháp:
Chia khối lập phương, nhận xét các khối tạo thành và tính thể tích của chúng
Cách giải:
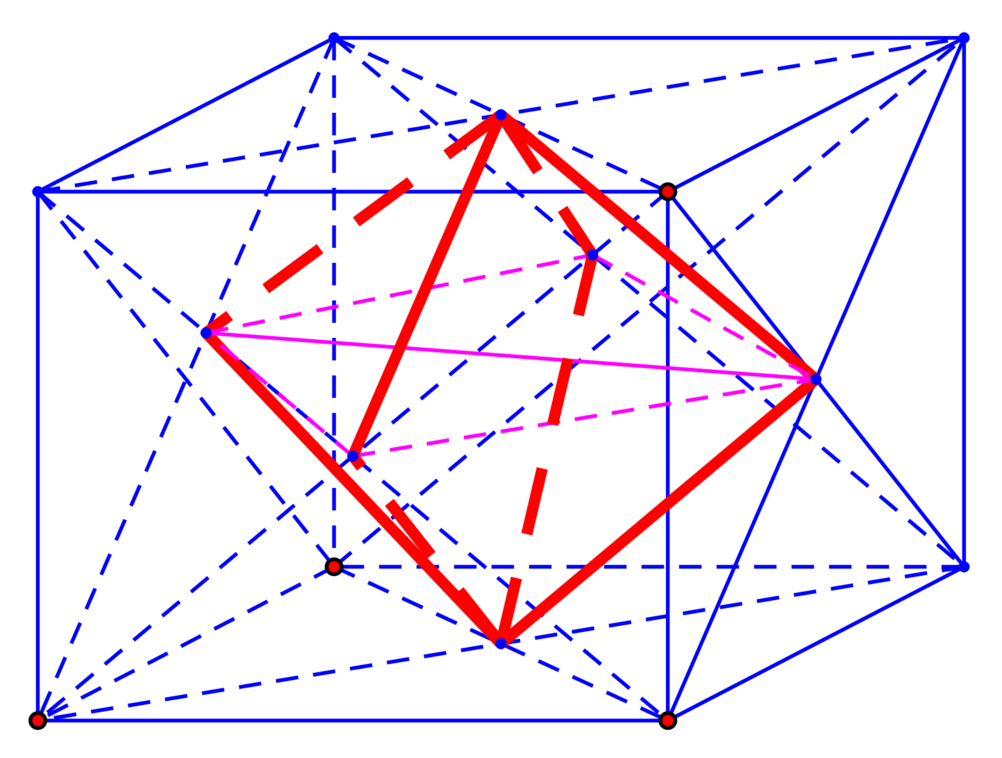
Chia khối lập phương ABC.A’B’C’ bởi mặt phẳng (AB’D’) và (C’BD) ta được:
+) Chóp A.A’B’D’
+) Chóp C’.BCD
+) Khối bát diện ABD.B’C’D’
Ta có
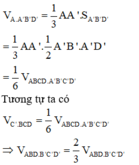
Các khối A.A’B’D’ và C’.BCD không phải là chóp tam giác đều và khối bắt diện ABD.B’C’D’ không phải là khói bát diện đều
Do đó chỉ có mệnh đề III đúng

Đáp án C
Khối đa diện đều loại {3;5} là khối 12 mặt đều, với các mặt tam giác đều bằng 1
diện tích tam giác đều là 3 4
Vậy diện tích cần tính là S = 12 . 3 4 = 3 3 .

Đáp án là A
Cạnh của hình bát diện đều bằng:
a 2 2 ⇒ S d a y = a 2 2 2 = a 2 2
Thể tích cần tính: V = 2 3 h . S d a y = 2 3 a 2 a 2 2 = a 3 6
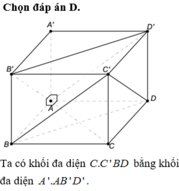

Chọn đáp án B.
Theo lý thuyết cơ bản về các khối đa diện đều ta có đáp án là B.