Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
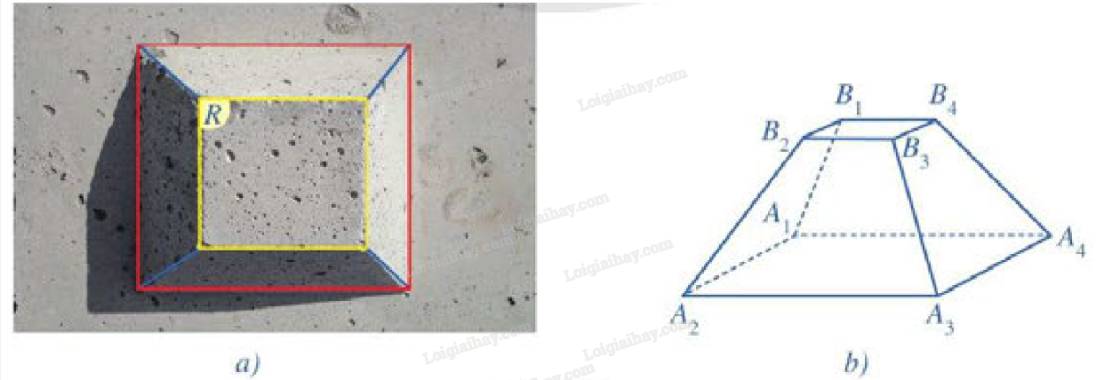
\(\begin{array}{l}\left( P \right)\parallel \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\\ \Rightarrow {A_1}^\prime {A_2}^\prime \parallel {A_1}{A_2},{A_2}^\prime {A_3}^\prime \parallel {A_2}{A_3},{A_3}^\prime {A_4}^\prime \parallel {A_3}{A_4},{A_4}^\prime {A_5}^\prime \parallel {A_4}{A_5},{A_5}^\prime {A_6}^\prime \parallel {A_5}{A_6},{A_6}^\prime {A_1}^\prime \parallel {A_6}{A_1}\\ \Rightarrow \frac{{{A_1}^\prime {A_2}^\prime }}{{{A_1}{A_2}}} = \frac{{{A_2}^\prime {A_3}^\prime }}{{{A_2}{A_3}}} = \frac{{{A_3}^\prime {A_4}^\prime }}{{{A_3}{A_4}}} = \frac{{{A_4}^\prime {A_5}^\prime }}{{{A_4}{A_5}}} = \frac{{{A_5}^\prime {A_6}^\prime }}{{{A_5}{A_6}}} = \frac{{{A_6}^\prime {A_1}^\prime }}{{{A_6}{A_1}}}\end{array}\)
Mà \({A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4} = {A_4}{A_5} = {A_5}{A_6} = {A_6}{A_1}\)
\( \Rightarrow {A_1}^\prime {A_2}^\prime = {A_2}^\prime {A_3}^\prime = {A_3}^\prime {A_4}^\prime = {A_4}^\prime {A_5}^\prime = {A_5}^\prime {A_6}^\prime = {A_6}^\prime {A_1}^\prime \)
Vậy đa giác \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \) là lục giác đều.
b) Ta có:
\(\left. \begin{array}{l}O' \in {A_1}^\prime {A_4}^\prime \subset \left( {S{A_1}{A_4}} \right)\\O' \in {A_3}^\prime {A_6}^\prime \subset \left( {S{A_3}{A_6}} \right)\\\left( {S{A_1}{A_4}} \right) \cap \left( {S{A_3}{A_6}} \right) = SO\end{array} \right\} \Rightarrow O' \in SO\)
Mà \(S.{A_1}{A_2}{A_3}...{A_6}\) là hình chóp đều \( \Rightarrow SO \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)
Vậy \(OO' \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)

a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:

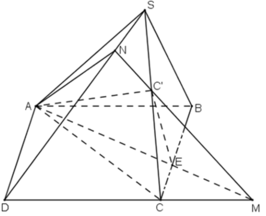
a) Giao điểm M của CD và mp(C’AE).
Trong mp(ABCD), d cắt CD tại M, ta có:
+ M ∈ CD
+ M ∈ d ⊂ (C’AE) ⇒ M ∈ (C’AE)
Vậy M là giao điểm của CD và mp(C’AE).
b) + Trong mặt phẳng (SCD), gọi giao điểm của MC’ và SD là N.
N ∈ MC’ ⊂ (C’AE) ⇒ N ∈ (C’AE).
N ∈ SD ⊂ (SCD) ⇒ N ∈ (SCD)
⇒ N ∈ (C’AE) ∩ (SCD).
⇒ (C’AE) ∩ (SCD) = C’N.
+ (C’AE) ∩ (SCB) = C’E.
+ (C’AE) ∩ (SAD) = AN.
+ (C’AE) ∩ (ABCD) = AE
Vậy thiết diện của hình chóp cắt bởi mặt phẳng (C’AE) là tứ giác C’NAE

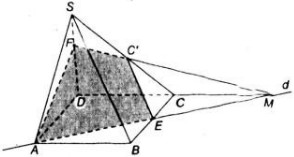
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE).
b)
Do M = DC ∩ (C'AE) nên M ∈ (SDC),.
Trong (SDC) : MC' ∩ SD = F.
Ta có:
\(\left(C'AE\right)\cap\left(SDC\right)=FC'\)
\(\left(C'AE\right)\cap\left(SAD\right)=AF\)
\(\left(C'AE\right)\cap\left(ABCD\right)=AE\)
\(\left(C'AE\right)\cap\left(SBC\right)=C'E\)
Vậy thiết diện là AEC'F.

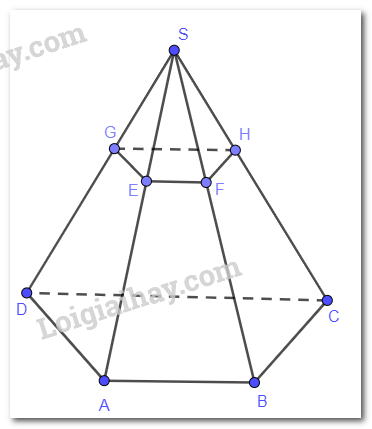
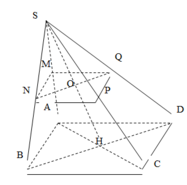
Mặt phẳng (SAD) chứa đường thẳng AD song song với mp(P) nên mặt phẳng (P) cắt (SAD) theo giao tuyến song song với AD. Vẽ EG // AD (G thuộc SD) thì EG là giao tuyến của (P) và (SAD).
Mặt phẳng (SAB) chứa đường thẳng AB song song với mp(P) nên mặt phẳng (P) cắt (SAB) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc SB) thì EF là giao tuyến của (P) và (SAB).
Ta có AB // CD, EF // AB suy ra CD // EF hay CD // mp(P)
Mặt phẳng (SCD) chứa đường thẳng CD song song với mp(P) nên mặt phẳng (P) cắt (SCD) theo giao tuyến song song với CD. Vẽ GH // CD (H thuộc SC) thì GH là giao tuyến của (P) và (SCD).
FH thuộc (P), FH thuộc (SBC) suy ra FH là giao tuyến của (P) và (SBC).
Tứ giác EFGH có EF // GH (vì cùng song song với CD) suy ra EFGH là hình thang.



Các đường thẳng này sẽ đồng quy tại 1 điểm.