Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời gian con chó chạy củng chính là thời gian từ lúc 2 cha con bắt đầu đi cho đến lúc gặp nhau
\(\Rightarrow t=\frac{s}{v_{cha}+v_{con}}=\frac{1}{4+6}=0,1h\)
Vậy quảng đường con chó đã chạy:
\(\Rightarrow s_{chó}=v_{chó}.t=10.0,1=1km\)
Vậy con chó đã chạy được quảng đường là 1km.

Chọn đáp án C
? Lời giải:
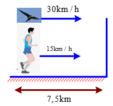
+ Con chim và vận động viên chuyển động cùng thời gian khi đến đích: t = s v = 7 , 5 15 = 0 , 5 h
+ Quãng đường di chuyển của con chim: s = 30.0 , 5 = 15 k m

Đáp án C.
Con chim và vận động viên chuyển động cùng thời gian khi đến đích:


Đáp án C.
Con chim và vận động viên chuyển động cùng thời gian khi đến đích: t = s v = 7 , 5 15 = 0 , 5 h
Quãng đường di chuyển của con chim: s = 30.0 , 5 = 15 k m

Chọn B.
Gọi t là thời gian xe chạy từ A đến B.
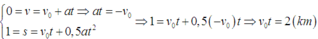
Quãng đường chó chạy được là: Scho = 4v0t = 8(km)

Gọi t là thời gian từ lúc 2xe xuất phát đến lúc 2xe gặp nhau cũng là thời gian con ong bay . (h;t>0)
Khi đó : Xe 1 đi được quãng đường là : S1=v1.t=30t(km)
Xe 2 đi được quãng đường là : S2=v2.t=50t(km)
Ta có : S=S1+S2
\(\Rightarrow\)120=30t+50t
\(\Rightarrow120=80t\)
\(\Rightarrow t=1,5\left(h\right)\)
\(\Rightarrow\)Quãng đường con ong bay là :
S3=v3.t=60.1,5=90(km)



\(\Rightarrow\left\{{}\begin{matrix}t1=\dfrac{S}{2+6}=\dfrac{3}{8}=0,375h\\t2=\dfrac{S}{3+5}=\dfrac{3}{8}=0,375h\end{matrix}\right.\)
\(\Rightarrow vtb=\dfrac{0,375\left(6+5\right)}{2.0,375}=5,5km/h\)
chon \(Ox\equiv AB,O\equiv A,\)(coi AB la khoang cach tu nha toi truong,)chieu(+) A->B
\(\Rightarrow\left\{{}\begin{matrix}x1=3t\\x2=3-2t\end{matrix}\right.\)\(\Rightarrow x1=x2\Rightarrow t=0,6h\)
\(\Rightarrow S=vtb.t=0,6.5,5=3,3km\)
mình mới tình ra chính xác là 3,43 bạn ơi