Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
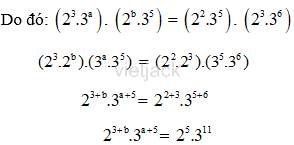
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y=
Mà xy =
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6

a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

a: \(\Leftrightarrow n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

Lời giải:
Vì $ƯCLN(a,b)=21$ nên đặt $a=21x, b=21y$ với $x,y$ là stn, $x,y$ nguyên tố cùng nhau.
Ta có:
$BCNN(a,b)=21xy=420\Rightarrow xy=20$ (1)
$a+21=b$
$\Rightarrow 21x+21=21y$
$\Rightarrow x+1=y$ (2)
Từ $(1); (2)$ và $x,y$ là 2 số nguyên tố cùng nhau nên $x=4, y=5$
$\Rightarrow a=21x=21.4=84; b=21y=21.5=105$

câu a; b cách làm tương tự nhau. Bạn xem câu ở câu hỏi tương tự: http://olm.vn/hoi-dap/question/89869.html
c) đề bài cho [a;b] + (a;b) = 15
gọi d = (a;b) => a = d.m; b = d.n ( coi m < n và m; n nguyên tố cùng nhau)
Ta có: [a;b] = \(\frac{a.b}{d}=\frac{dm.dn}{d}=d.m.n\)
khi đó, d.mn + d = 15 => d(m.n + 1) = 15 => m.n + 1 \(\in\) Ư(15) mà m.n + 1 > 2
=> m.n + 1 \(\in\) {3;5;15}
+) m.n + 1 = 3 => m.n = 2 = 1.2 => m = 1; n = 2 và d = 5 => a = 5.1 = 5; b = 5.2 = 10
+) m.n + 1 = 5 => m.n = 4 = 1.4 => m = 1; n = 4 và d = 3 => a = 3.1 = 3; b = 3.4 = 12
+) m.n + 1 = 15 => m.n = 14 =1 .14 = 2.7
m =1; n = 14 ; d = 1 => a= 1; b = 14
m = 2; n = 7 ;d = 1 => a = 2; b = 7
Vậy....

Ta có: UCLN(a;b) = 15 => a = 15m và b = 15n (Với m ; n khác 0)
Ta lại có: BCNN(a;b) = 300
Mà: a . b = BCNN(a;b) . UCLN(a;b)
=> a . b = 300 . 15 = 4500 (*)
Ta thay a = 15m và b = 15n vào (*) ta được: 15m . 15n = 4500
=> 225 . mn = 4500 => mn = 4500 : 225 => mn = 20
Do: m và n là sso tự nhiên nên mn = 4 . 5 = 1 . 20
+) Với m = 4 và n = 5 thì a = 60 và b = 75
+) Với m = 5 và n = 4 thì a = 75 và b = 60
+) Với m = 1 và n = 20 thì a = 15 và b = 300
+) Với m = 20 và n = 1 thì a = 300 và b = 15
Ta có : ƯCLN ( a , b ) = 15 => a = 15m và b = 15n ( m ; n \(\ne\) 0 ).
Ta lại có : BCNN ( a ; b ) = 300
Mà a . b = BCNN ( a ; b ) . ƯCLN ( a ; b )
=> a . b = 300 . 15 = 4500 (*)
Thay a = 15m và b = 15n vào (*) ta được :
15m . 15n = 4500
<=> ( 15 . 15 ) mn = 4500
<=> 225mn = 4500
<=> mn = 4500 : 225
<=> mn = 20
Do m và n là số tự nhiên nên mn = 4 . 5 = 1 . 20
=> Ta có bảng :
| m | 4 | 5 | 1 | 20 |
| n | 5 | 4 | 20 | 1 |
| a | 60 | 75 | 15 | 300 |
| b | 75 | 60 | 300 | 15 |

Ta có: \(ƯCLN\left(a,b\right)=15\Rightarrow a=15m\) và \(b=15n\)(Với \(m;n\ne0\))
Ta lại có: \(BCNN\left(a,b\right)=300\)
Mà: a . b = BCNN(a;b) . UCLN(a;b)
=> a . b = 300 . 15 = 4500 (*)
Ta thay a = 15m và b = 15n vào (*) ta được: 15m . 15n = 4500
=> 225 . mn = 4500 => mn = 4500 : 225 => mn = 20
Do: m và n là sso tự nhiên nên mn = 4 . 5 = 1 . 20
+) Với m = 4 và n = 5 thì a = 60 và b = 75
+) Với m = 5 và n = 4 thì a = 75 và b = 60
+) Với m = 1 và n = 20 thì a = 15 và b = 300
+) Với m = 20 và n = 1 thì a = 300 và b = 15
Ta có: ƯCLN(a,b)=15⇒a=15mƯCLN(a,b)=15⇒a=15m và b=15nb=15n(Với m;n≠0m;n≠0)
Ta lại có: BCNN(a,b)=300BCNN(a,b)=300
Mà: a . b = BCNN(a;b) . UCLN(a;b)
=> a . b = 300 . 15 = 4500 (*)
Ta thay a = 15m và b = 15n vào (*) ta được: 15m . 15n = 4500
=> 225 . mn = 4500 => mn = 4500 : 225 => mn = 20
Do: m và n là sso tự nhiên nên mn = 4 . 5 = 1 . 20
+) Với m = 4 và n = 5 thì a = 60 và b = 75
+) Với m = 5 và n = 4 thì a = 75 và b = 60
+) Với m = 1 và n = 20 thì a = 15 và b = 300
+) Với m = 20 và n = 1 thì a = 300 và b = 15

Do ƯCLN(a; b) = 15 => a = 15.m; b = 15.n (m;n)=1
=> BCNN(a; b) = 15.m.n = 300
=> m.n = 300 : 15 = 20
Giả sử a > b => m > n mà (m;n)=1 => \(\left[\begin{array}{nghiempt}m=20;n=1\\m=5;n=4\end{array}\right.\)
+ Với m = 20; n = 1 thì a = 20.15 = 300; b = 1.15 = 15
+ Với m = 5; n = 4 thì a = 5.15 = 75; b = 4.15 = 60
Vậy các cặp giá trị (a;b) thỏa mãn đề bài là: (300;15) ; (75;60) ; (60;75) ; (15;300)
Khi nào số tự nhiên n được gọi là bội chung của hai số a và b ?
Trả lời : Khi số tự nhiên n chia hết cho cả a và b
Bội chung nhỏ nhất của a và b là số như thế nào?
Trả lời : Bội chung nhỏ nhất của a và b là số nguyên dương nhỏ nhất chia hết cho a và b