Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Theo bài ra ta có: \(i = 50^\circ ,{\rm{ }}{n_1}\; = 1,{\rm{ }}{n_2}\; = 1,33\) thay vào \(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\) ta được:
\(\begin{array}{l}\frac{{\sin {{50}^o}}}{{\sin r}} = \frac{{1,33}}{1}\,(r \ne 0)\\ \Rightarrow \sin r = \frac{{\sin {{50}^o}}}{{1,33}} \approx 0,57597\,\,(TM)\\ \Leftrightarrow \left[ \begin{array}{l}r \approx {35^o}10' + k{360^o}\\r \approx {180^o} - {35^o}10' + k{360^o}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}r \approx {35^o}10' + k{360^o}\\r \approx {144^o}50' + k{360^o}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Mà \({0^o} < r < {90^o} \Rightarrow r \approx {35^o}10'\)
Vậy góc khúc xạ \(r \approx {35^o}10'\)
tham khảo:
a) Bóng của cây cột trên sân có thể được nhìn như là hình chiếu của cây cột qua phép chiếu song song với tia nắng mặt trời.
b) Khi tia sáng mặt trời vuông góc với mặt sân, bóng của cây cột sẽ không xuất hiện trên mặt sân vì không có tia sáng nào có thể chiếu trực tiếp lên bề mặt sân để tạo ra bóng của cây cột.
Gọi A là biến cố “Xạ thủ thứ i bắn trúng bia”, i=1,2
TH1. Xạ thủ thứ nhất bắn trúng, xạ thủ 2 bắn trượt thì xác suất là:
P A 1 = 1 2 . 1 − 1 3
TH2. Xạ thủ thứ nhất bắn trượt, xạ thủ thứ 2 bắn trúng thì xác suất là:
P A 2 = 1 − 1 2 . 1 3
TH3. Cả 2 xạ thủ đều bắn trượt
P A 3 = 1 − 1 2 . 1 − 1 3
Xác suất của biến cố Y là:
P Y = P A 1 + P A 2 + P A 3 = 5 6
Đáp án. D
Đáp án D
Gọi X là biến cố: “Không có xạ thủ nào bắn trúng mục tiêu”.
Khi đó P( X ) = P( A ).P( B ).P( C ) = 0,3.0,4.0,5=0,14
=> P(X) = 1- P( X )=0,94.
=> Chọn đáp án D.
a. Sau 1 chu kì bán rã: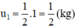 
Sau 2 chu kì bán rã: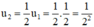 
Sau 3 chu kì bán rã: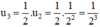 
…
Tổng quát : Sau n chu kì bán rã :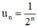 
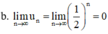
c. Chất phóng xạ không còn độc hại nữa khi khối lượng chất phóng xạ còn lại < 10-6 g = 10-9 kg
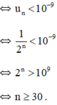
Vậy sau 30 chu kì = 30.24000 = 720 000 năm thì 1kg chất phóng xạ này không còn độc hại nữa.
Đáp án B.
Xác suất để xạ thủ thứ nhất bắn không trúng bia là:
Xác suất để xạ thủ thứ hai bắn không trúng bia là:
Gọi biến cố A:
Có ít nhất một xạ thủ không bắn trúng bia
. Khi có biến cố A có 3 khả năng xảy ra:
* Xác suất người thứ nhất bắn trúng bia, người thứ hai không bắn trúng bia là 
* Xác suất người thứ nhất không bắn trúng bia, người thứ hai bắn trúng bia là 
.
* Xác suất cả hai người đều bắn không trúng bia là 
.
Vậy 
.
Đáp án D
Phương pháp:
A, B là các biến cố độc lập thì P(A.B) = P(A).P(B)
Chia bài toán thành các trường hợp:
- Một người bắn trúng và một người bắn không trúng,
- Cả hai người cùng bắn không trúng.
Sau đó áp dụng quy tắc cộng.
Cách giải:
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 - 1 2 = 1 2
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 - 1 3 = 2 3
Gọi biến cố A:”Có ít nhất một xạ thủ không bắn trúng bia ”.
Khi đó biến cố A có 3 khả năng xảy ra:
+) Xác suất người thứ nhất bắn trúng bia, người thứ hai không bắn trúng bia: 1 2 . 2 3 = 1 3
+) Xác suất người thứ nhất không bắn trúng bia, người thứ hai bắn trúng bia: 1 2 . 1 3 = 1 6
+) Xác suất cả hai người đều bắn không trúng bia:
Khi đó
Gọi A là biến cố “Xạ thủ thứ i bắn trúng bia” i = 1,2.
Khi đó, P(A1) =1/2; P(A2) = 1/3; A1 và A2 độc lập với nhau
X =A1∩ A2 nên P(X) = P(A1∩ A2) = P(A1.A2) = P(A1).P(A2) = 1/6
Chọn đáp án là B
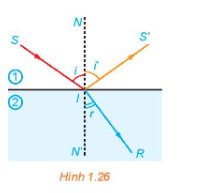
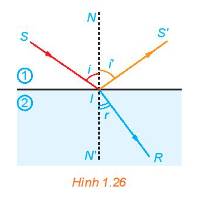
tHAM KHẢO: