Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Đặt m là khối lượng tấm ván, ∆m là khối lượng hòn đá. Do cả hai trường hợp đều trượt đều (a = 0) nên ta có:
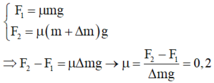

(0,25 điểm) Cho biết: F = 2000 (N), μ = 0,04, lấy g = 10 (m/ s 2 ), a = 0 Tìm m = ?
(0,25 điểm) Giải: Áp dụng định luật II Niu Tơn: 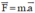
Với 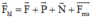
(0,25 điểm) 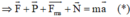
(0,25 điểm):
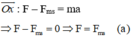
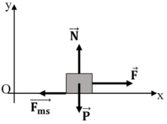
(0,25 điểm): 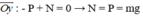
Lực ma sát: Fms = μN = μ.m.g (b)
(0,25 điểm) Thay (b) vào (a)
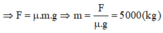

Chọn B.
Đặt m là khối lượng tấm ván, ∆m là khối lượng hòn đá. Do cả hai trường hợp đều trượt đều (a = 0) nên ta có:

Có thể giải thích cho mik tại sao lại ra 0,2 được không. Sao mik thay số vào ko đc

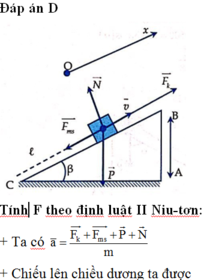
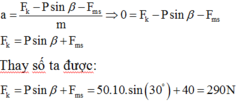
Công của lực kéo F theo phương song song với mặt phẳng nghiêng khi xe lên hết dốc là
![]()

xe lăn khối lượng m được kéo lực F thì chuyển động đều
F-Fms=0\(\Leftrightarrow\)2=\(\mu.m.g\) (2)
khi chất lên xe lăn m1, được kéo bằng lực F' thì chuyển động đều
\(F'-F'_{ms}=0\Leftrightarrow3=\mu.\left(m+m_1\right).g\) (1)
lấy (1) chia (2)
\(\dfrac{3}{2}=\dfrac{m+m_1}{m}\)\(\Rightarrow m=4kg\)
thay m vào (1) koặc (2)
\(\Rightarrow\)\(\mu\)=0,05

a)Vật chuyển động thẳng đều:
Lực ma sát:
\(F_{ms}=\mu mg=0,1\cdot5\cdot10=5N\)
\(\Rightarrow F_k=P=10m=10\cdot5=50N\)
b)Sau khi chuyển động đc 2s:
Vật chuyển động trên mặt phẳng nằm ngang thì theo định luật ll Niu-tơn ta có:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
Gia tốc vật: \(S=\dfrac{1}{2}at^2\Rightarrow a=\dfrac{2S}{t^2}=\dfrac{2\cdot5}{2^2}=2,5\)m/s2
Chọn chiều dương là chiều chuyển động.
\(\Rightarrow F-F_{ms}=m\cdot a\)
\(\Rightarrow F=m\cdot a+F_{ms}=5\cdot2,5+5=17,5N\)
Tóm tắt: \(F=60N;m=20kg;F'=100N;g=10\)m/s2
\(\mu=?\)
Bài giải:
Ta có: \(\overrightarrow{F_k}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
Khi \(F=60N\) thì vật chuyển động đều\(\left(a=0\right)\):
\(\Rightarrow\mu.m.g=60\Rightarrow\mu.m=60:10=6\left(1\right)\)
Khi chất thêm một kiện hàng thì \(F'=100N\) vật chuyển động đều:
\(\Rightarrow\mu\left(m+20\right)g=100\Rightarrow\mu\left(m+20\right)=\dfrac{100}{10}=10\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\mu=0,2\)