Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi số đo hai cung lệch nhau k.2π (k ∈ Z) thì điểm cuối của chúng có thể trùng nhau.
Chẳng hạn các cung α = π/3 và β = π/3 + 2π , γ = π/3 - 2π có điểm cuối trùng nhau khi biểu diễn trên đường tròn lượng giác.

Trường hợp này xảy ra khi chúng sai khác nhau bội của 3600 (hay bội của 2π)

Đáp án: C
Ta có:

Vậy cung (I) và (III) có điểm cuối trùng nhau

Chọn A.
Ta có: 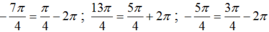
Suy ra chỉ có hai cung 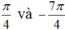 có điểm cuối trùng nhau.
có điểm cuối trùng nhau.

Chọn A.
Theo giả thiết ta có: ![]()
suy ra điểm M là điểm chính giữa của cung phần tư thứ I.

Ta có Sđ cung AB = 15 + k2π, k ∈ Z
15 + k2π < 0 ⇔ k < -15/2π
Vậy với k = -3 ta được cung AB có số đo âm lớn nhất là 15 - 6π

Ta có số đo cung \(AB=15+k2\pi,k\in\mathbb{Z}\)
\(15+k2\pi< 0\Leftrightarrow k< -\dfrac{15}{2\pi}\)
Vậy với \(k=-3\) ta được cung AB có số đo âm lớn nhất là \(15-6\pi\)

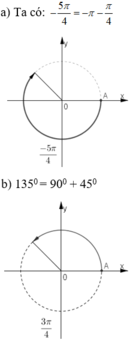
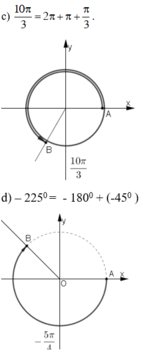
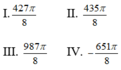

Chọn C.
Ta có 42000 = - 1200 + 12. 3600
nên cung có số đo – 1200 có ngọn cung trùng với ngọn cung có số đo 42000.