Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
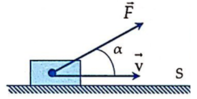
Ta có góc tạo bởi hướng của lực và phương chuyển động s là α = F → , s → ^ = 30 0
=> Công của lực tác dụng: A = F s cos α = 150.20. c o s 30 0 ≈ 2598 J
Đáp án: B

Áp dụng công thức tính công : A = Fscosα ta được.
Công của lực F1 : A1 = 750.15. 2 2 = 7931,25 J.
Công của lực F2: A2 = 750.15. 1 2 = 5625 J

Đổi:1phút=60s
Ta có:
S = v 0 t + 1 2 a t 2 → a = 2 S t 2 = 2.2700 60 2 = 1 , 5 m / s 2
Lực cản tác dụng vào vật bằng:
F−FC=ma→FC=F−ma=15−2,5.1,5=11,25N
Đáp án: A

Tham khảo

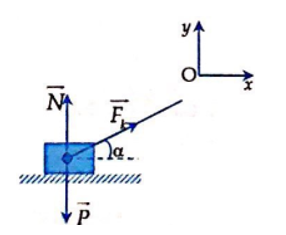
Theo định luật \(II\) Niuton, ta có:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m\overrightarrow{a}\)
Chiếu lên xOy, ta có:
\(Ox:F.\cos\) \(a\) \(=150.\cos30=75\sqrt{3N}\)
Do \(\left(\overrightarrow{P};\overrightarrow{s}\right)=90\) nên \(Ap=0\)
Do \(\left(\overrightarrow{F_{ms}};\overrightarrow{s}\right)=180\) nên \(A_{F_{ms}}.s=-75\sqrt{3.20}=-1500\sqrt{3}\left(J\right)\)

Định luật ll Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{F_k}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
Oy: \(N=P-Fsin\alpha\)
Ox: \(Fcos\alpha-\mu mg=m\cdot a\)
\(\Rightarrow a=\dfrac{Fcos\alpha-\mu mg}{m}=\dfrac{5cos30-0,2\cdot1\cdot10}{1}=2,33\)m/s2
Quãng đường vật sau 4s: \(S=\dfrac{1}{2}at^2=\dfrac{1}{2}\cdot2,33\cdot4^2=18,64m\)
Vận tốc sau 4s: \(v=a\cdot t=2,33\cdot4=9,32\)m/s
(sai bạn ạ)\(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{Fk}+\overrightarrow{Fms}=m\overrightarrow{a}\)\(\left(lấy-g=\dfrac{10m}{s^2}\right)\)
\(chiếuOy\Rightarrow N=P-F_k.sin30^o\)
\(chiếu-Ox\Rightarrow F_k.cos30^o-F_{ms}=ma\Rightarrow a^{ }=5.cos30^o-\mu\left(mg-F_k.sin30^o\right)=2,8m/s^2\)
\(\Rightarrow S=\dfrac{1}{2}at^2=22,4m\)
\(\Rightarrow v=\sqrt{2aS}=\sqrt{2.22,4.2,8}=11,2m/s\)
\(b,\)\(\Rightarrow a_{max}\Rightarrow a=\dfrac{F_k.cos\left(\alpha\right)-\mu\left(mg-F_k.sin\left(\alpha\right)\right)}{m}\)
\(a=5.cos\left(\alpha\right)-10\mu+\mu.5.sin\left(\alpha\right)=5\left[cos\left(\alpha\right)+\mu.sin\left(\alpha\right)\right]-2\)
\(\Rightarrow a_{max}\Leftrightarrow\left[cos\left(\alpha\right)+\mu.sin\left(\alpha\right)\right]_{max}\)
\(\Rightarrow\left[cos\left(\alpha\right)+\mu.sin\left(\alpha\right)\right]^2\le\left(1+\mu^2\right)\left[sin^2\left(\alpha\right)+cos^2\left(\alpha\right)\right]\le\left(1+0,2^2\right)=1,04\Rightarrow\left[cos\left(\alpha\right)+\mu sin\left(\alpha\right)\right]\le\sqrt{1,04}=1,01\Rightarrow a_{max}\Leftrightarrow\dfrac{1}{cos\left(\alpha\right)}=\dfrac{0,2}{sin\left(\alpha\right)}\Rightarrow\alpha=.....\)