Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

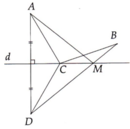
Lấy D là điểm đối xứng, với A qua d. Theo tính chất đường trung trực: CA = CD.
Do đó CA + CB = CD + CB.
Gọi M là giao điểm của BD và d.
Nếu C không trùng với M thì xét tam giác BCD, ta có: CB + CD > BD hay CA + CB > BD (1).
Nếu C trùng với M thì:
CA + CB = MA + MB = MD + MB = BD (2).
So sánh (1) và (2) ta thấy điểm C trùng M hay C là giao điểm của BD và d thì giá trị của tổng CA + CB là nhỏ nhất.
Chú ý: Điểm C tìm được ở vị trí M như vậy là điểm duy nhất. Thật vậy, nếu lấy E đối xứng với B qua d thì AE vẫn cắt d ở M đúng vị trí mà BD cắt d.

x y A B C M
Lấy M sao cho xy là trung trực của AM
điểm C thuộc xy => CA = CM => CA + BC = CM + BC
Theo bất đẳng thức tam giác, trong tam giác CBM có CM + BC \(\ge\) BM
=> AC + BC \(\ge\) BM
vậy AC + BC ngắn nhất = BM khi B; C; M thẳng hàng
=> C là giao của BM và đường thằng xy thì tổng AC + BC ngắn nhất
Mọi người làm nhanh jup mik nhé, ai có đáp án sẽ k luôn. Kamsa =)
kkk em mới học lớp 7