Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

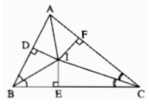
Kẻ: ID⊥AB, IE⊥BC, IF⊥AC
Xét hai tam giác vuông ΔIBD và ΔIEB, ta có:
∠(DBI) =∠(EBI) (gt)
∠(IDB) =∠(IEB) =90o
BI cạnh chung
Suy ra: ΔIDB= ΔIEB(cạnh huyền, góc nhọn)
Suy ra: ID = IE ( hai cạnh tương ứng)
Xét hai tam giác vuông ΔIEC và ΔIFC, ta có:
∠(ECI) =∠(FCI)
∠(IEC) =∠(IFC) =90o
CI cạnh huyền chung
Suy ra: ΔIEC= ΔIFC(cạnh huyền góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông ΔIDA và ΔIFA, ta có:
ID=IF
∠(IDA) =∠(IFA) =90o
AI cạnh huyền chung
Suy ra: ΔIDA= ΔIFA(cạnh huyền.cạnh góc vuông)
Suy ra: ∠(DAI) =∠(FAI) (hai góc tương ứng)
Vậy AI là tia phân giác góc A

A B C I M N P
Gọi M,N,P lần lượt là hình chiếu của I lên các cạnh BC,BA,CA
Xét \(\Delta\)BIN và \(\Delta\)BIM có
\(\widehat{IBN}=\widehat{IBM}\)(BI là phân giác)
BI chung
=> \(\Delta\)BIN = \(\Delta\)BIM (cạnh huyền-góc nhọn)
=> IM=IN
CM tương tự có: \(\Delta\)CIP=\(\Delta\)CIM => IM=IP
=> IM=IN=IP
Xét \(\Delta\)AIN và \(\Delta\)AIP vuông tại N và P có:
IA chung
IN=IM
=> \(\Delta\)AIN = \(\Delta\)AIP (cạnh huyền -cạnh góc vuông)
=> \(\widehat{IAN}=\widehat{IAP}\)=> IA là phân giác góc A (DPCM)

1.Vì các tia phân giác của các góc B và C cắt nhau tại I
\(\Rightarrow\)I là giao của các đường phân giác trong tam giác
\(\Rightarrow\)AI là tia phân giác của góc A
1.
Kẻ: \(ID\perp AB;IE\perp BC;IF\perp AC\)
\(\widehat{IDB}=\widehat{IEB}=90^0\)
\(\widehat{DBI}=\widehat{EIB}\left(gt\right)\)
BI cạnh huyền chung
⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\widehat{IEC}=\widehat{IFC}=90^0\)
\(\widehat{ECI}=\widehat{FCI}\left(gt\right)\)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
\(\widehat{IDA}=\widehat{IFA}=90^0\)
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra\(\widehat{DAI}=\widehat{FAI}\) (hai góc tương ứng)
Vậy AI là tia phân giác của \(\widehat{A}\)

A B C D E I F
Kẻ ID \(\perp\) AB, IE \(\perp\) BC, IF \(\perp\) AC
Xét hai tam giác vuông IBD và IBE có:
IB: cạnh chung
\(\widehat{DBI}=\widehat{EBI}\) (gt)
Vậy: \(\Delta IBD=\Delta IBE\left(ch-gn\right)\)
\(\Rightarrow\) ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông ICF và ICE có:
IC: cạnh chung
\(\widehat{FCI}=\widehat{ECI}\) (gt)
Vậy: \(\Delta ICF=\Delta ICE\left(ch-gn\right)\)
\(\Rightarrow\) IF = IE (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông AID và AIF có:
AI: cạnh chung
ID = IF (cmt)
Vậy: \(\Delta AID=\Delta AIF\left(ch-cgv\right)\)
\(\Rightarrow\widehat{IAD}=\widehat{IAF}\) (hai góc tương ứng)
Do đó: AI là tia phân giác của \(\widehat{A}\).

( bạn tự vẽ hình)
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
tao không biết con ngu
cậu đừng nói thế công chúa o ri , ko bt làm thì thui , lại còn chửi ngta , bài này e ko bt làm chị thông cảm nhé ! E là Hs tiểu học thui