Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(3^{r1}=3^1=3\)
\(3^{r2}\simeq3^{1.4}\simeq\text{4 , 655536722}\)
\(3^{r3}\simeq3^{1.41}\simeq\text{4 , 706965002}\)
\(3^{r4}=3^{1.4142}\simeq4,\text{72873393}\)
\(3^{\sqrt{2}}=\text{4 , 728804388}\)
b: \(\left|3^{\sqrt{2}}-3^{r1}\right|=\text{4 , 728804388 − 3 = 1 , 728804388 }\)
\(\left|3^{\sqrt{2}}-3^{r2}\right|=\text{4,728804388-4,655536722=0,07326766609}\)
\(\left|3^{\sqrt{2}}-3^{r3}\right|=\text{4,728804388 − 4,706965002 = 0,02183938612 }\)
\(\left|3^{\sqrt{2}}-3^{r4}\right|=\text{4,728804388−4,72873393=0,0000704576662}\)
=>Khi n càng tăng dần thì sai số tuyệt đối càng giảm

a: \(r_6=3^{\text{1 , 414213 }}=4,7288\text{01466}\)
\(r_7=3^{\text{ 1 , 4142134}}=\text{4,728803544}\)
b: Khi \(n\rightarrow+\infty\) thì \(3^{r_n}\rightarrow3^{\sqrt{2}}\)

Tham khảo:
a,

\(\lim f\left( {{x_n}} \right) = \lim \left( {2.\frac{{n + 1}}{n}} \right) = \lim 2.\lim \left( {1 + \frac{1}{n}} \right) = 2.\left( {1 + 0} \right) = 2\)
b) Lấy dãy số bất kì \(\left( {{x_n}} \right),{x_n} \to 1\) ta có \(f\left( {{x_n}} \right) = 2{x_n}.\)
\(\lim f\left( {{x_n}} \right) = \lim \left( {2{x_n}} \right) = \lim 2.\lim {x_n} = 2.1 = 2\)

1: \(\lim\limits_{n\rightarrow\infty}\left(\sqrt[3]{n^3+n^2+n+1}-n\right)\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{n^3+n^2+n+1-n^3}{\sqrt[3]{\left(n^3+n^2+n+1\right)^2}+n\cdot\sqrt[3]{n^3+n^2+n+1}+n^2}\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{n^2+n+1}{n^2\cdot\sqrt[3]{\left(1+\dfrac{1}{n}+\dfrac{1}{n^2}+\dfrac{1}{n^3}\right)^2}+n^2\cdot\sqrt[3]{1+\dfrac{1}{n}+\dfrac{1}{n^2}+\dfrac{1}{n^3}}+n^2}\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{1+\dfrac{1}{n}+\dfrac{1}{n^2}}{\sqrt[3]{\left(1+\dfrac{1}{n}+\dfrac{1}{n^2}+\dfrac{1}{n^3}\right)^2}+\sqrt[3]{1+\dfrac{1}{n}+\dfrac{1}{n^2}+\dfrac{1}{n^3}}+1}\)
\(=\dfrac{1}{1+1+1}=\dfrac{1}{3}\)
2: \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{n^2+n}-\sqrt{n^2-n+1}\right)\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{n^2+n-n^2+n-1}{\sqrt{n^2+n}+\sqrt{n^2-n+1}}\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{2n-1}{\sqrt{n^2+n}+\sqrt{n^2-n+1}}\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{2-\dfrac{1}{n}}{\sqrt{1+\dfrac{1}{n}}+\sqrt{1-\dfrac{1}{n}+\dfrac{1}{n^2}}}\)
\(=\dfrac{2}{1+1}=\dfrac{2}{2}=1\)

\(\left|0,992\right|< 1\) ; \(\left|0,866\right|< 1\) nên \(lim\left(u_n\right)=lim\left(r_n\right)=0\)

Ta sẽ chứng minh dãy bị chặn trên bởi 2
Thật vậy, với \(n=1;2\) thỏa mãn
Giả sử điều đó cũng đúng với \(n=k\) , tức \(u_k< 2\)
Ta cần chứng minh \(u_{k+1}< 2\)
Ta có: \(u_{k+1}=\sqrt{3u_k-2}< \sqrt{3.2-2}=2\) (đpcm)
Tương tự, ta cũng quy nạp được dễ dàng \(u_n>1\)
Mặt khác: \(u_n-u_{n-1}=\sqrt{3u_{n-1}-2}-u_{n-1}=\dfrac{3u_{n-1}-2-u_{n-1}^2}{\sqrt{3u_{n-1}-2}+u_{n-1}}\)
\(=\dfrac{\left(2-u_{n-1}\right)\left(u_{n-1}-1\right)}{\sqrt{3u_{n-1}-2}+u_{n-1}}>0\)
\(\Rightarrow u_n>u_{n-1}\Rightarrow\) dãy tăng
Dãy tăng và bị chặn trên nên có giới hạn hữu hạn.
Gọi giới hạn đó là k thì:
\(k=\sqrt{3k-2}\Leftrightarrow k=2\)

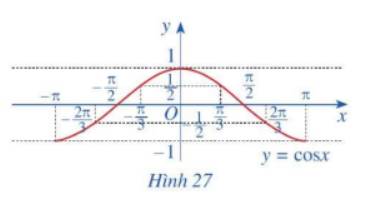
a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
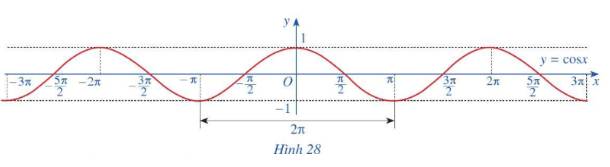
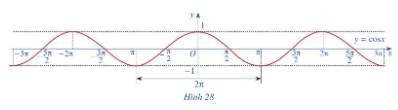
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

a/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2+1-x^2}{\sqrt{x^2+1}-x}+\lim\limits_{x\rightarrow-\infty}\dfrac{3x^3-1-x^3}{\sqrt[3]{\left(3x^3-1\right)^2}+x\sqrt[3]{3x^3-1}+x^2}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{1}{x}}{-\sqrt{\dfrac{x^2}{x^2}+\dfrac{1}{x^2}}-\dfrac{x}{x}}+\lim\limits_{x\rightarrow-\infty}\dfrac{-\dfrac{1}{x^2}}{\dfrac{\sqrt[3]{\left(3x^3-1\right)^2}}{x^2}+\dfrac{x\sqrt[3]{3x^3-1}}{x^2}+\dfrac{x^2}{x^2}}=0\)
b/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2+x-x^2}{\sqrt{x^2+x}+x}+\lim\limits_{x\rightarrow+\infty}\dfrac{x^3-x^3+x^2}{x^2+x\sqrt[3]{x^3-x^2}+\sqrt[3]{\left(x^3-x^2\right)^2}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{x}{x}}{\sqrt{\dfrac{x^2}{x^2}+\dfrac{x}{x^2}}+\dfrac{x}{x}}+\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{x^2}{x^2}}{\dfrac{x^2}{x^2}+\dfrac{x\sqrt[3]{x^3-x^2}}{x^2}+\dfrac{\sqrt[3]{\left(x^3-x^2\right)^2}}{x^2}}\)
\(=\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6}\)
c/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{2x-1-2x-1}{\sqrt[3]{\left(2x-1\right)^2}+\sqrt[3]{4x^2-1}+\sqrt[3]{\left(2x+1\right)^2}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-\dfrac{2}{x^{\dfrac{2}{3}}}}{\dfrac{\sqrt[3]{\left(2x-1\right)^2}}{x^{\dfrac{2}{3}}}+\dfrac{\sqrt[3]{4x^2-1}}{x^{\dfrac{2}{3}}}+\dfrac{\sqrt[3]{\left(2x+1\right)^2}}{x^{\dfrac{2}{3}}}}=0\)
Check lai ho minh nhe :v
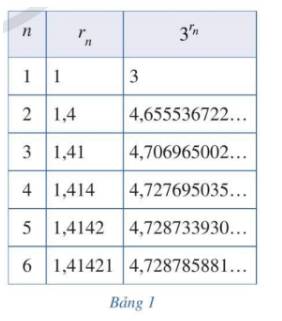


Từ hàng thứ 5 trở đi, số \(3^{r_n}\) càng gần với giá trị 4,728... Làm tròn đến hàng phần trăm, ta được \(3^{\sqrt{2}}\approx4,73\).