Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình \(\left(C_m\right)\) viết lại:
\(y=\left(x-m+2\right)^3-3\left(x-m+2\right)\)
Họ đồ thị hàm \(\left(C_m\right)\) đơn giản là đồ thị hàm \(y=x^3-3x\) tịnh tiến song song với trục Ox, do đó họ đồ thị này luôn tiếp xúc với các tiếp tuyến tại cực trị của \(y=x^3-3x\) (là hai đường thẳng \(y=\pm2\))
Vậy họ đường cong \(\left(C_m\right)\) luôn tiếp xúc với 2 đường thẳng cố định \(y=\pm2\)

Giả sử \(M\left(x_0;y_0\right)\) là điểm mà họ \(\Delta_{\alpha}\) không đi qua. Khi đó phương trình sau vô nghiệm với mọi m : \(m^2-2\left(x^3_0+x_0\right)m+y_0+x^2_0-x_0-2=0\)
\(\Leftrightarrow\Delta'=\left(x^3_0+x_0\right)^2-\left(y_0+x^2_0-x_0-2\right)< 0\)
\(\Leftrightarrow y_0>x^6_0+2x^4_0+x_0+2\)
Xét phương trình : \(2mx^3-x^2+\left(2m+1\right)x-m^2+2=x^6+2x^4+x+2\)
\(\Leftrightarrow m^2-2\left(x^3+x\right)m+\left(x^3+x\right)^2=0\)
\(\Leftrightarrow\left(x^3+x-m\right)^2=0\) (*)
Vì phương trình \(x^3+x-m=0\) luôn có nghiệm nên (*) luôn có nghiệm bội.
Vậy \(\left(C_m\right)\) luôn tiếp xúc với đường cong \(y=x^6+2x^4+x+2\)
Khi đó:
hay
Cách 2: Gọi
Hay
Xét đường biên:
Lập phương trình hoành độ giao điểm ta được:
Phương trình này luôn có 1 nghiệm kép nên (dm) luôn tiếp xúc (P)

1.
Pt hoành độ giao điểm: \(\frac{2x-3}{x+3}=x-1\)
\(\Leftrightarrow2x-3=x^2+2x-3\)
\(\Leftrightarrow x=0\Rightarrow y=-1\)
Vậy tung độ giao điểm là \(-1\)
2.
\(y'=4x^3+4x\Rightarrow\left\{{}\begin{matrix}y'\left(1\right)=8\\y\left(1\right)=3\end{matrix}\right.\)
Pttt: \(y=8\left(x-1\right)+3=8x-5\)
3.
\(y'=3x^2-6x\)
Lấy y chia y' và lấy phần dư ta được pt đường thẳng là: \(y=-2x+1\)

Giả sử \(\left(C_m\right)\) luôn tiếp xúc với đường thẳng \(y=ax+b\), khi đó phương trình sau có nghiệm với mọi m :
\(\begin{cases}\frac{\left(3m+1\right)x+m-m^2}{x+m}=ax+b\\\frac{4m^2}{\left(x+m\right)^2}=a\end{cases}\) \(\Leftrightarrow\begin{cases}3m+1-\frac{4m^2}{x+m}=a\left(x+m\right)am+b\\\frac{4m^2}{\left(x+m\right)^2}=a\end{cases}\)
\(\Leftrightarrow\begin{cases}\frac{8m^2}{x+m}=am+3m+1-b\\\frac{4m^2}{\left(x+m\right)^2}=a\end{cases}\) \(\Leftrightarrow\frac{\left(am+3m+1-b\right)^2}{16m^2}=a\) với mọi m
\(\Leftrightarrow\left(a^2-10a+9\right)m^2+2\left(a+3\right)\left(1-b\right)m+\left(1-b\right)^2=0\) với mọi m
\(\Leftrightarrow\begin{cases}a^2-10a+9=0\\\left(a+3\right)\left(1-b\right)=0\\\left(1-b\right)^2=0\end{cases}\)
\(\Leftrightarrow\begin{cases}a=1;a=9\\b=1\end{cases}\)
Vậy \(\left(C_m\right)\) luôn tiếp xúc với 2 đường thẳng \(y=x+1;y=9x+1\)

a) Hàm có cực đại, cực tiểu khi mà $y'=-3x^2+2(m-1)x=x[2(m-1)-3x]$ có ít nhất hai nghiệm phân biệt $\Leftrightarrow 2(m-1)-3x=0$ có một nghiệm khác $0$ hay $m\neq 1$
b) Đồ thị hàm số $(\star)$ cắt trục hoành tại ba điểm phân biệt khi mà phương trình $y=-x^3+(m-1)x^2-m+2=0$ có $3$ nghiệm phân biệt
$\Leftrightarrow (1-x)[x^2+x(2-m)+(2-m)]=0$ có ba nghiệm phân biệt
$\Leftrightarrow x^2+x(2-m)+(2-m)=0$ có hai nghiệm phân biệt khác $1$
Do đó ta cần có $\left\{\begin{matrix}1+2-m+2-m=5-2m\neq 0\\ \Delta =(2-m)^2-4(2-m)>0\end{matrix}\right.$
Vậy để thỏa mãn đề bài thì $m\neq \frac{5}{2}$ và $m>2$ hoặc $m<-2$
c) Gọi điểm cố định mà đồ thị hàm số đi qua là $(x_0,y_0)$
$y_0=-x_0^3+(m-1)x_0^2-m+2$ $\forall m\in\mathbb{R}$
$\Leftrightarrow m(x_0^2-1)-(x_0^3+x_0^2+y_0-2)=0$ $\forall m\in\mathbb{R}$
$\Rightarrow\left{\begin{matrix}x_0^2=1\\ x_0^3+x_0^2+y_02=0\end{matrix}\right.\begin{bmatrix}(x_0,y_0)=(1;0)\\ (x_0,y_0)=(-1;2)\end{bmatrix}$
Viết lại đoạn cuối:
$\Rightarrow\left{\begin{matrix}x_0^2=1\\x_0^3+x_0^2+y_0-2=0\end{matrix}\right.$ $\Rightarrow \begin{bmatrix}(x_0,y_0)=(1;0)\\ (x_0,y_0)=(-1;2)\end{bmatrix}$

Bài 1:
ĐTHS \(y=x^3+3mx+1\) có hai điểm cực trị khi \(y'=3x^2+3m=0\Leftrightarrow x^2+m=0\) có hai nghiệm phân biệt \(\Leftrightarrow m<0\)
Hoành độ của hai điểm cực trị chính là hai nghiệm của PT \(x^2+m=0\)
Khi đó ta có \(y=x^3+3mx+1=x(x^2+m)+2mx+1=2mx+1\)
Do đó \(d: y=2xm+1\) là đường thẳng đi qua hai điểm cực trị
\(\Rightarrow d(M,d)=\frac{|1-3|}{\sqrt{(2m)^2+1}}=\frac{2}{\sqrt{5}}\Leftrightarrow m^2=1\rightarrow m=-1\) (do \(m<0\))
Vậy $m=-1$
Bài 2:
ĐTHS trên có hai điểm cực trị khi \(y'=6x^2+6(m-1)x+6(m-2)=0\)
\(\Leftrightarrow 6[x+(m-2)](x+1)=0\) có hai nghiệm phân biệt.
Khi đó, chỉ cần \(m\neq 3\)
Từ pt trên ta thu được hai nghiệm \(x=2-m;x=-1\)
Điểm CĐ và CT nằm trong khoảng \((-2,3)\) suy ra
\(\left\{\begin{matrix} -1\in (-2;3)\\ 2-m\in (-2;3)\end{matrix}\right.\Leftrightarrow 4>m>-1\)
Vậy \(4>m>-1\) và \(m\neq 3\)
Bài 3:
Ta có \(y'=x^2-2(m+1)x+2m+1=0\)
\(\Leftrightarrow [x-(2m+1)](x-1)=0\)
ĐTHS có cực trị khi PT trên có hai nghiệm phân biệt, tức là \(m\neq 0\)
Khi đó, hai nghiệm thu được là \(1\) và \(2m+1\) .
Hiển nhiên các điểm cực trị của ĐTHS là \((1;m-1);\left(2m+1,\frac{-4m^3}{3}+m-1\right)\)
Điểm cực trị của ĐTHS thuộc trục hoành thì tung độ bằng $0$
Nếu \((1;m-1)\) là điểm cực đại thì \(\left\{\begin{matrix} m-1=0\\ m-1>\frac{-4m^3}{3}+m-1\end{matrix}\right.\Rightarrow m=1\)
Nếu \(\left (2m+1,\frac{-4m^3}{3}+m-1\right)\) là điểm cực đại thì
\(\left\{\begin{matrix} \frac{-4}{3}m^3+m-1=0\\ m-1<\frac{-4m^3}{3}+m-1\end{matrix}\right.\Rightarrow m<0\) (không thỏa mãn)
Vậy $m=1$
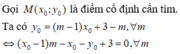
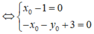
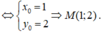
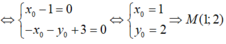
Do đó phương trình đường thẳng đi qua hai điểm cực trị là
Đường thẳng AB đi qua gốc tọa độ