Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

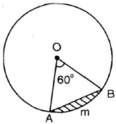
Tam giác OAB là tam giác đều có cạnh R= 5,1 cm.
Công thức tính diện tích tam giác đều cạnh a là: 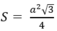
Do đó, diện tích tam giác đều OAB cạnh OA= R = 5,1 cm là: 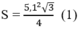
Diện tích hình quạt tròn AOB là:
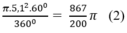
Từ (1) và (2) suy ra diện tích hình viên phân là:
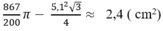

Tam giác OAB là tam giác đều có cạnh R= 5,1 cm.
Công thức tính diện tích tam giác đều cạnh a là: 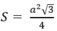
Do đó, diện tích tam giác đều OAB cạnh OA= R = 5,1 cm là: 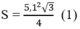
Diện tích hình quạt tròn AOB là:
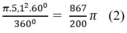
Từ (1) và (2) suy ra diện tích hình viên phân là:
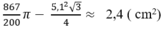
Kiến thức áp dụng
+ Diện tích tam giác đều cạnh a là:
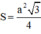
+ Diện tích hình quạt tròn bán kính R, cung nº được tính theo công thức:
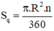

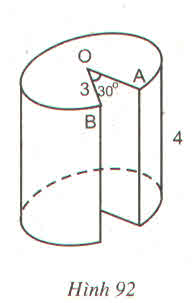
góc AOB=180-60=120 độ
S OAB=1/2*OA*OB*sinAOB=\(R^2\cdot\dfrac{\sqrt{3}}{4}\)
S q OAB=\(pi\cdot R^2\cdot\dfrac{120}{360}=pi\cdot R^2\cdot\dfrac{1}{3}\)
=>\(Svp=R^2\left(pi\cdot\dfrac{1}{3}-\dfrac{\sqrt{3}}{4}\right)\)


Gọi MN = 2R là đường kính của đường tròn có cung tròn là ![]()
Theo bài tập 23, ta có:
KA. KB = KM. KN
hay KA. KB = KM. (2R - KM)
Thay số, ta có:
20. 20 = 3(2R - 3)
do đó 6R = 400 + 9 = 4099.
Vậy R = ≈688,2(mét)

Giải:
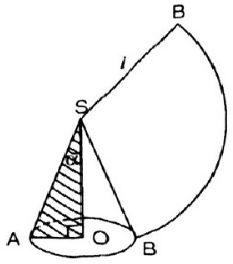
Diện tích hình quạt :
Diện tích xung quanh của hình nón: Sxq = π.r.l
Theo đầu bài ta có: Sxq= Sq => π.r.l=
Vậy l = 4r
Suy ra sin(a) = = 0,25
Vậy a = 14o28’
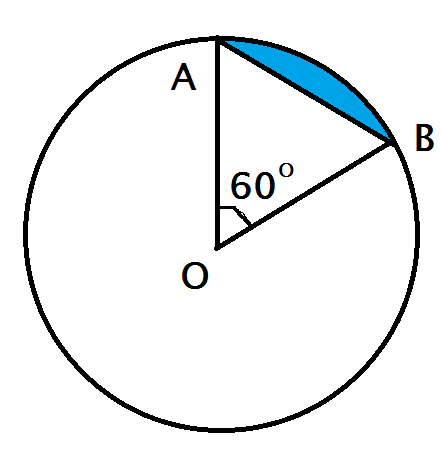
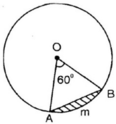



Hướng dẫn giải:
∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là a2√44 ta có
S∆OBC = SΔOBC=R2√34 (1)
Diện tích hình quạt tròn AOB là:
π.R2.6003600=πR26 (2)
Từ (1) và (2) suy ra diện tích hình viên phân là:
πR26−R2√34=R2(π6−√34)
Thay R = 5,1 ta có Sviên phân ≈ 2,4 (cm2)