Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Dễ thấy rằng mỗi mặt phẳng đối xứng của tứ diện đều luôn chứa một cạnh của tứ diện và đi qua trung điểm cạnh đối diện.
Suy ra tứ diện đều có 6 mặt phẳng đối xứng

Đáp án D
Dựa vào hình tứ diện đều và khái niệm mặt phẳng đối xứng của khối đa diện.
Mặt phẳng tạo bởi hai đỉnh bất kì và trung điểm của cạnh đối là mặt phẳng đối xứng của tứ diện đều.
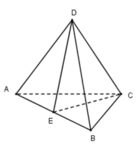
Tứ diện đều có 4 đỉnh. Vậy có C 4 2 = 6 mặt phẳng đối xứng.

Đáp án B
Giả sử ta có tứ diện đều ABCD, mặt phẳng đối xứng của tứ diện ABCD chính là các mặt phẳng trung trực ứng với từng cạnh của tứ diện ấy.
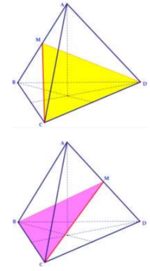
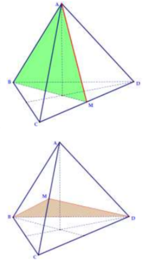
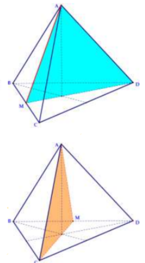

Phương pháp:
Sử dụng lý thuyết khối đa diện để làm bài toán.
Cách giải:
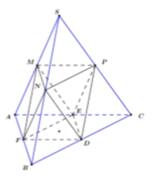
Khối đa diện được tạo từ 6 đỉnh là 6 trung điểm của các cạnh của tứ diện đều là khối bát diện đều có 6 đỉnh, 12 cạnh và 8 mặt.
Khối bát diện đều là khối đa diện có 9 mặt đối xứng.
Chọn: D

Đáp án C
Tứ diện đều có 6 mặt phẳng đối xứng là các mặt phẳng nối trung điểm của môt cạnh với cạnh đối của nó.

Đáp án là C
Mỗi mặt phẳng đối xứng của tứ diện đều là mặt phẳng đi qua trung điểm 1 cạnh và chứa cạnh đối diện của tứ diện đều có 6 cạnh nên số mặt phẳng đối xứng là 6

Đáp án C
Tứ diện đều có mặt phẳng đối xứng là mặt phẳng tạo bởi một cạnh với trung điểm của cạnh đối diện nó.
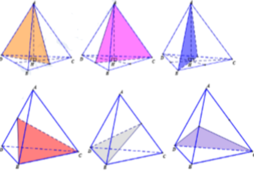
Đáp án D
Có tất cả 6 mặt phẳng. Đó là các mặt phẳng đi qua 1 cạnh và trung điểm của cạnh đối diện.