Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: NF=15cm
Xét ΔMNF vuông tại M có sin MFN=MN/NF=3/5
nên góc MFN=37 độ
=>góc MNF=53 độ
\(MO=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cn\right)\)
\(FO=\dfrac{12^2}{15}=9.6\left(cm\right)\)
b: Xét ΔMFN và ΔFEM có
góc MFN=góc FEM
góc FNM=góc EMF
Do đó: ΔMFN đồng dạng với ΔFEM
Suy ra:MF/FE=MN/MF
hay \(MF^2=MN\cdot FE\)

1)
a) Áp dụng định lí Pytago vào ΔMNF vuông tại M, ta được:
\(NF^2=MF^2+MN^2\)
\(\Leftrightarrow NF^2=9^2+12^2=225\)
hay NF=15(cm)
Xét ΔMNF vuông tại M có
\(\sin\widehat{MFN}=\dfrac{MN}{NF}=\dfrac{9}{15}=\dfrac{3}{5}\)
hay \(\widehat{MFN}\simeq37^0\)
\(\Leftrightarrow\widehat{MNF}=53^0\)

hoicj tốtttttttttttttttttttttttttttttttttttttttttttttttt


Hình thang MNEF vuông tại M, F có EF là đáy lớn. Hai đường chéo ME và NF vuông góc với nhau tại O
a) Cho biết MN = 9cm và MF = 12cm, Hãy giải tam giác MNF,
MN=9;MF=12; FN=√9^2+12^2)=3.√(9+16)=15
^F=actan(3/4)
^N=artan(4/3)
S=1 /2.9.12=54
hm=2S/NF=36/5
...
tính MO
MO=hm=36/5
và FO,
FO=√MF^2-MO^2)=9√(1-4^2/5^2)=27/5
kẻ NF ????? vuông góc với EF tại H.

a: NF=15cm
Xét ΔMNF vuông tại M có sin MFN=MN/NF=3/5
nên góc MFN=37 độ
=>góc MNF=53 độ
b: \(MO=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cn\right)\)
\(FO=\dfrac{12^2}{15}=9.6\left(cm\right)\)
c: \(S_{EOF}=\dfrac{OF\cdot OE}{2}\)
FE=12^2/9=16cm
\(OE=\dfrac{16^2}{20}=\dfrac{256}{20}=12.8\left(cm\right)\)
\(S_{EOF}=\dfrac{12.8\cdot9.6}{2}=12.8\cdot4.8=61.44\left(cm^2\right)\)

a: NF=15cm
Xét ΔMNF vuông tại M có sin MFN=MN/NF=3/5
nên góc MFN=37 độ
=>góc MNF=53 độ
b: \(MO=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cn\right)\)
\(FO=\dfrac{12^2}{15}=9.6\left(cm\right)\)
c: \(S_{EOF}=\dfrac{OF\cdot OE}{2}\)
FE=12^2/9=16cm
\(OE=\dfrac{16^2}{20}=\dfrac{256}{20}=12.8\left(cm\right)\)
\(S_{EOF}=\dfrac{12.8\cdot9.6}{2}=12.8\cdot4.8=61.44\left(cm^2\right)\)

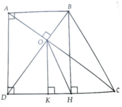
a, Tính được DB=15cm. A D B ^ ≈ 37 0 ; A B D ^ ≈ 53 0
b, Tính được AO=7,2cm, DO=9,6cm và AC=20cm
c, Kẻ OK ⊥ DC tại K
DH=AB=9cm, DC=16cm, DK=5,76cm và OK=7,68cm
Từ đó S D O H = O K . D H 2 = 7 , 68 . 9 2 = 34,56 c m 2

c) Xét tứ giác FMHN có
\(\widehat{NFM}=90^0\)
\(\widehat{FNH}=90^0\)
\(\widehat{FMH}=90^0\)
Do đó: FMHN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Hình chữ nhật FMHN có đường chéo FH là tia phân giác của \(\widehat{NFM}\)(gt)
nên FMHN là hình vuông(Dấu hiệu nhận biết hình vuông)

a,i, Tính được NF=15cm; M F N ^ ≈ 37 0 và M N F ^ = 53 0
ii, Tìm được MO = 36 5 cm, FO = 48 5 cm
iii, Tìm được S F N E = 96 c m 2
Cách 1: Ta có S F O H S F N E = F O F N . F H F E = 9 25
=> S ∆ F O H = 34 , 56 c m 2
Cách 2: Gợi ý. Kẻ đường cao OK của ∆FOH => S ∆ F O H = 34 , 56 c m 2
b, Ta có ∆MFN ~ ∆FEM(g.g) => M F F E = M N F M <=> M F 2 = M N . F E