Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chiều cao TG ABC: 27,5x2:(8+3)=5cm
DT TG ABC là 3x5:2=7,5cm2
tk nha

Giải:
Trung bình cộng 2 đáy là :
(6 + 3) : 2= 4,5 ( cm )
Chiều cao của hình thang ABCD là:
28,8 : 4,5= 6,4 ( cm)
Diện tích hình tam giác ABC là:
( 3 x 6,4) : 2= 9,6( cm2)
Đáp số : 9,6 cm2

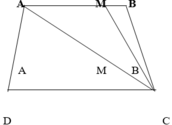
Đáy mới AM là: 15 – 5 = 10 (cm)
Tổng hai đáy AM và CD là : 10 + 20 = 30 (cm)
Chiều cao hình thang ABCD là : 280 x 2 : 5 = 112 (cm)
Diện tích hình thang ABCD là : 30 x 112 : 2 = 1680 (cm2)
Cách 2
Nối A với C
Ta có đoạn AM là : 15 – 5 = 10 (cm)
Diện tích tam giác ACM gấp 2 lần điện tích tam giác MCB Þ Diện tích tam giác ACM = 280 x 2 = 560 (cm2) (vì AM gấp BM hai lần và đường cao hai tam giác bằng nhau)
∆ DAC và ∆ MCB có :
DC gấp MB là
20 : 5 = 4 ( lần)
Đường cao chung nên diện tích tam giác DAC gấp diện tích tam giác
MCB 4 lần.
Diện tích tam giác ADC là : 280 x 4 = 1120 (cm2)

Bài 4: Chiều cao AH là:
72×2:18=8 (cm)
Diện tích hình thang ABCD là:
(12+18)×8:2=120 (cm2)
Đáp số: 120 cm2

Đáy lớn \(DC\): \(6.\frac{3}{2}=9cm\)
Ta có: \(S_{ABCD}=\frac{\left(AB+DC\right).AH}{2}=93cm^2\)
Thay: \(S_{ABCD}=\frac{\left(6+9\right).AH}{2}=93cm^2\)
\(\Rightarrow AH=\frac{93.2}{15}=12,4cm\)
Lại có: \(AB//CD\Rightarrow AH=DN=12,4cm\)
\(S_{ABD}=\frac{1}{2}DN.AB=\frac{1}{2}.12,4.6=37,2cm^2\)
Vậy ...........
Chiều cao của hình thang ABCD là:
\(27.5\cdot2:\left(8+3\right)=55:11=5\left(cm\right)\)
TH1: AB=8cm
=>\(S_{ABD}=\dfrac{1}{2}\cdot5\cdot8=4\cdot5=20\left(cm^2\right)\)
TH2: AB=3cm
=>\(S_{ABD}=\dfrac{1}{2}\cdot5\cdot3=\dfrac{15}{2}=7,5\left(cm^2\right)\)