Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

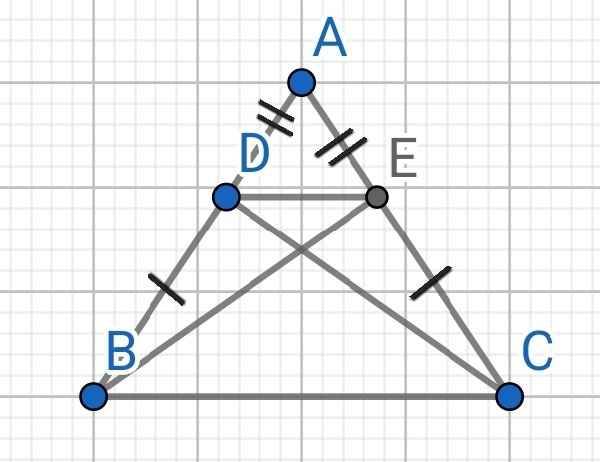 a) Xét ∆AEB và ∆ADC có:
a) Xét ∆AEB và ∆ADC có:
AB = AC (gt)
∠A chung
AE = AD (gt)
⇒ ∆AEB = ∆ADC (c-g-c)
⇒ BE = DC (hai cạnh tương ứng)
b) Đề sai, ghi lại đề đi em!

Xét tam giác ABD có
E là trung điểm AD
P là trung điểm BD
=> EP là đường trung bình của tam giác ABD (1)
Xét tam giác ABC có :
Q là trung điểm AC
F là trung điểm CB
=> QF là đường trung bình của tam giác ABC (2)
Xét tứ giác ABCD có :
Q là trung điểm AC
P là trung điểm BD
=> QP là đường trung bình của tứ giác ABCD (3)
Từ (1) ; (2) ; (3)
=> Q , F , E , P thẳng hàng

Bạn ơi câu a hình như bạn ghi sai đề rồi, phải là chứng Minh DC bằng EB chứ. Bạn xem lại hộ mình nhé nếu có gì mình xin lỗi ha
Nếu là đề sai theo mình là như vậy nè:
xét 2 Tam giác ABE và ACD có:
AE = AC (gt)
AB = AD(gt)
Â1 = Â2 (đối đỉnh)
suy ra Tam giác ABE = Tam giác ADC
Câu b
Vì 2 Tam giác ở câu a ta mới chứng Minh là bằng nhau nên ta có:
bạn tự vẽ hình và kí hiệu hình nhăn
ta có: góc D1 = góc B1 (2 góc tương ứng)
mà 2 góc này ở vị tí so le trong
suy ra BC // DE

Xét hình thang ABCD(AB//CD) có
M là trung điểm của AD
N là trung điểm của BC
Do đó: MN là đường trung bình
=>MN//AB//CD và \(MN=\dfrac{AB+CD}{2}\)