Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tính chiều cao của hình thang
Trong tam giác ADC có: AD2 + AC2 = 52 + 122 = 169
CD2 = 132 = 169
=> AD2 + AC2 = CD2 => tam giác ADC vuông tại A
Kẻ đường cao AH (H thuộc CD)
Ta có: AH.CD = AD.AC => \(AH=\frac{AD.AC}{CD}=\frac{5.12}{13}=\frac{60}{13}cm\)
b) cm AB = CD/2
\(S_{ABCD}=\frac{AH.\left(AB+CD\right)}{2}=45\Rightarrow AB=\frac{45}{\frac{AH}{2}}-CD=\frac{45}{\frac{60}{13}:2}-13=\frac{13}{2}cm\)
=> AB = CD/2

a) Theo định lí Pytago đảo, vì \(CD^2=AD^2+AC^2\) nên ΔACD vuông tai A ⇒ \(S_{ACD}=\frac{5.12}{2}=30cm^2\)
⇒ \(S_{ABC}=S_{ABCD}-S_{ACD}\)\(=15cm^2\)
Gọi AH là chiều cao hình thang
⇒ \(AH=\frac{S_{ACD}.2}{13}=\frac{60}{13}cm\)
b) Từ phần a), ta có:
\(AB=\frac{S_{ABC}.2}{AH}=\frac{30}{\frac{60}{13}}=6,5cm\)
⇒ \(AB=\frac{1}{2}CD\)

Ta áp dụng công thức Brahmagupta để tính
\(s=\frac{\sqrt{\left(AB^2+CD^2+BD^2+AC^2\right)+8\cdot AB\cdot CD\cdot BD\cdot AC-2\left(AB^4+CD^4+BD^4+AC^4\right)}}{4}\)
A) Thay số vào ta đc \(S=6\sqrt{55}\approx44,4972\left(cm^2\right)\)
b) \(S\approx244,1639\left(cm^2\right)\)
hok tốt ...
Công thức Brahmagupta là công thức tính diện tích của một tứ giác nội tiếp (tứ giác mà có thể vẽ một đường tròn đi qua bốn đỉnh của nó) mà hình thang ko có đường tròn nào đi qua đủ bốn đỉnh của nó nên công thức này ko được áp dụng vào bài này

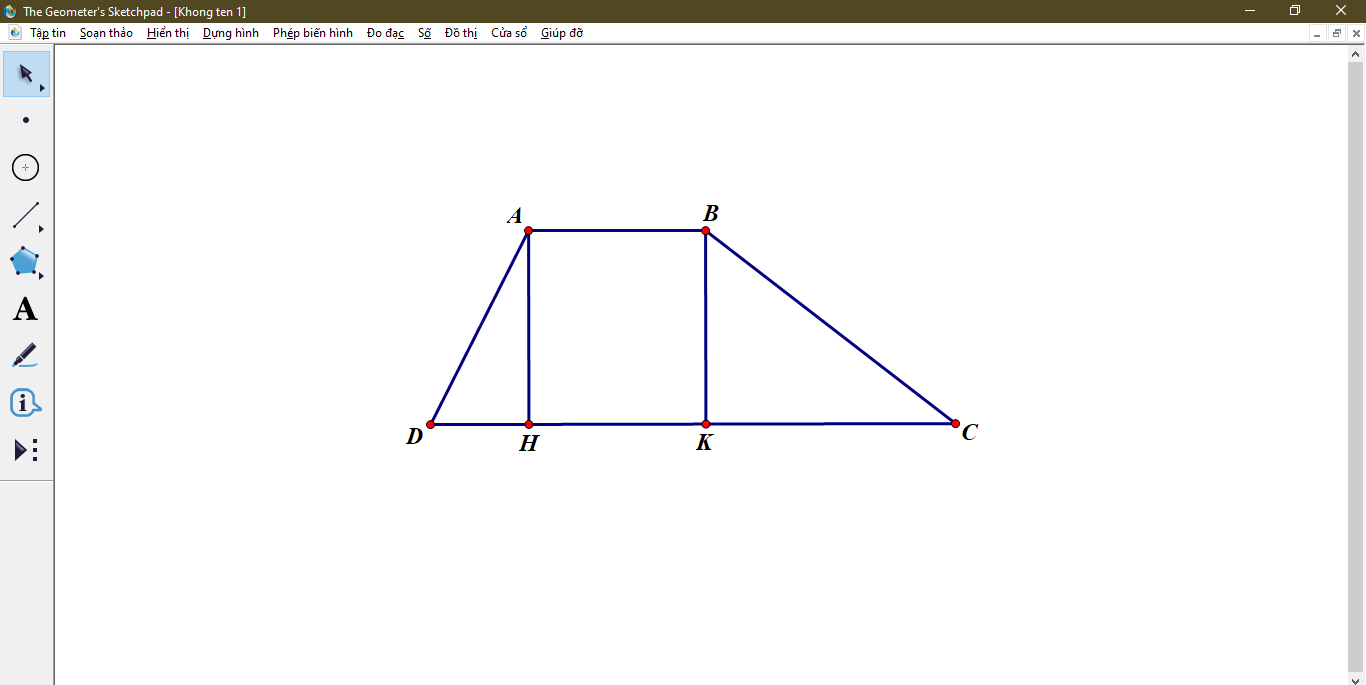
Kẻ đường cao AH và đường cao BK . ⇒AB=HK=1cm
Nên ta có : DH+CK=4 (1)
Theo tỉ số lượng giác cho tam giác ADH và BCK ta lại có :
\(\left\{{}\begin{matrix}AH=tan60\cdot DH\\BK=tan30\cdot CK\end{matrix}\right.\)\(\Rightarrow tan60\cdot DH=tan30\cdot CK\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình :
\(\left\{{}\begin{matrix}DK+CK=4\\\sqrt{3}DH-\dfrac{\sqrt{3}}{3}CK=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DH=1\\CK=3\end{matrix}\right.\)
\(\Rightarrow AH=tan60\cdot DH=\sqrt{3}\cdot1=\sqrt{3}\left(cm\right)\)
\(\Rightarrow S_{ABCD}=12\cdot AH\cdot\left(AB+CD\right)=12\cdot\sqrt{3}\cdot\left(1+5\right)=3\sqrt{3}\left(cm^2\right)\)
Tick hộ nha bạn 😘