Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao 4cm.
Áp dụng định lí Pi-ta-go ta tính được nửa đường chéo của hình vuông đáy là 3 (cm)
Suy ra, đường chéo của đáy là 6 (cm)
Diện tích đáy bằng: 1/2 .6.6 = 18( c m 2 )
Thể tích của hình chóp là: V =1/3 .S.h = 1/3 .18.4 = 24 ( c m 3 )
Vậy chọn đáp án B.

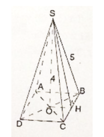
a) Ta có
OC2 = SC2 - SO2 (Pytago)
= 52 - 42 = 9(cm)
=> OC = 3(cm)
=> AC = 6(cm)
AB2 + BC2 = AC2 (pytago)
2BC2 = AC2 (do AB = BC)
BC2 = AC2/2 = 36/2 = 18(cm)
BC = √18 = 3√2 (cm)
Gọi K là trung điểm của BC. Tam giác SBC cân tại S có SH là đường trung tuyến nên SH cũng là đường cao. Suy ra SH ⊥ BC
Do đó
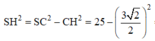
![]()

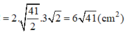
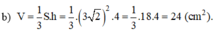

Diện tích đáy là:
60:5=12(cm2)
ĐỘ dài cạnh đáy là căn 12=2căn 3(cm)

gọi các cạnh đáy của hình chóp là ABC vì ΔABC đều => AB=AC=BC=4cm
kẻ đường thẳng đi qua A ⊥ BC tại M
=> AM là đường cao của tam giác => \(\widehat{AMB}=\)90o
=> AM là đường trung tuyến ( tc Δ đều)
=> BM=CM=BC/2=4/2=2cm
xét ΔAMB có \(\widehat{AMB}=\)90o
=> AM2+BM2=AB2 (đl pitago)
=>AM2+22=42
=> AM=\(2\sqrt{3}\)
=> V của hình chóp = \(\dfrac{2\sqrt{3}.4}{2}.6.\dfrac{1}{3}\)=\(8\sqrt{3}\)cm3 => Đáp án B

a, Xét tam giác ABC có:
AC2+AB2=242+182=900=302=BC2AC2+AB2=242+182=900=302=BC2⇒⇒ Tam giác ABC vuông tại A
Xét tam giác ABC và MDC có:
DMCˆ=BACˆDMC^=BAC^
CˆC^ là góc chung
⇒⇒ Tam giác ABC ~MDC ( g.g)
b, Vì tam giác ABC~MDC ⇒ABAC=MDMC=34⇒MD=3MC4⇒ABAC=MDMC=34⇒MD=3MC4ACBC=MCDC=45⇒DC=5MC4ACBC=MCDC=45⇒DC=5MC4
Mà:
ABMD=BCDC=ACMC=AB+BC+ACMD+DC+MC=723MC4+5MC4+4MC4ABMD=BCDC=ACMC=AB+BC+ACMD+DC+MC=723MC4+5MC4+4MC4=7212MC3⇒12MC=72.3=216⇒MC=18cm=7212MC3⇒12MC=72.3=216⇒MC=18cm⇒MD=3.184=13,5cm⇒MD=3.184=13,5cm
⇒DC=5.184=22,5cm

Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao 4cm.
Áp dụng định lí Pi-ta-go ta tính được nửa đường chéo của hình vuông đáy là 3cm.
Suy ra, đường chéo của đáy là 6cm
Diện tích đáy bằng :
Thể tích hình chóp là:
(B) 24cm3