Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
bn tham khảo tại đây nhé :
Bài 57 Sách bài tập - tập 2 - trang 98 - Toán lớp 8 | Học trực tuyến
tuy ko giống hết nhưng bn có thể dựa vào đó mà tham khảo
* Trường hợp góc B nhọn:
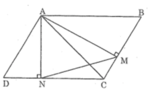
Xét △ AMB và △ AND, ta có:
∠ (AMB) = ∠ (AND) = 90 0
B = D (t/chất hình bình hành) ⇒ △ AMB đồng dạng △ AND (g.g)
Suy ra: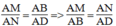 
Mà AD = BC (t/chất hình hình hành)
Suy ra: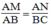 
Lại có: AB // CD (gt)
AN ⊥ CD (gt)
Suy ra: AN ⊥ AB hay ∠ (NAB) = 90 0
suy ra: ∠ NAM + ∠ MAB = 90 0 (1)
Trong tam giác vuông AMB ta có ∠ ABM = 90 0
Suy ra: ∠ (MAB) + ∠ B = 90 0 (2)
Từ (1) và (2) suy ra: ∠ NAM = ∠ B
Xét △ ABC và △ MAN ta có:
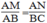(chứng minh trên)
∠ (NAM) = ∠ B (chứng minh trên)
Vậy △ ABC đồng dạng △ MAN (c.g.c)
* Trường hợp góc B tù:
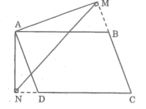
Xét △ MAN và △ AND, ta có:
∠ (AMB) = ∠ (AND) = 90 0
∠ (ABM) = ∠ (ADN) (vì cùng bằng C)
⇒ △ AMB đông dạng △ AND (g.g)
Suy ra: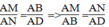
Mà AD = BC (t/chẩt hình bình hành)
Suy ra: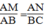 
Vì AB //CD nên ∠ (ABC) + ∠ C = 180 0 (3)
Tứ giác AMCN có ∠ (AMC) = ∠ (AND) = 90 0
Suy ra: ∠ (MAN) + ∠ C = 180 0 (4)
Từ (3) và (4) suy ra: (MAN) = (ABC)
Xét △ AMN và △ ABC, ta có:
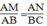(chứng minh trên)
∠ (MAN) = ∠ (ABC) (chứng minh trên)
Vậy △ MAN đồng dạng △ ABC (c.g.c)
a: Xét ΔAIB vuông tại I và ΔAEC vuông tại E có
góc IAB chung
=>ΔAIB đồng dạng vơi ΔAEC
b: ΔAIB đồng dạng với ΔAEC
=>AI/AE=AB/AC
=>AI/AB=AE/AC
=>ΔAIE đồng dạng với ΔABC và AB*AE=AI*AC
c: Xét ΔFAC vuông tại F và ΔICB vuông tại I có
góc FAC=góc ICB
=>ΔFAC đồng dạng với ΔICB
=>AF/IC=CA/CB
=>AF*CB=CA*IC
=>AB*AE+AF*CB=AC^2