Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(a\perp\left(Q\right)\)
b: Hai mặt phẳng (P) và (Q) có vuông góc với nhau

a: Gọi \(A,B\in a\)
A',B' lần lượt là hình chiếu của A,B trên (P)
\(d\subset\left(P\right)\) nên \(AB\subset\left(P\right)\)
=>d vuông góc A'A
Do đó: nếu d vuông góc a' thì d vuông góc mp(a,a')
=>d vuông góc a
b: Nếu d vuông góc a thì d vuông góc mp(a,a')
=>d vuông góc a'

Tham khảo
Vì sàn nhà là một mặt phẳng vuông góc với đường thẳng d. Mà đường thẳng a luôn nằm trên mặt phẳng đó nên đường thẳng d luôn vuông góc với đường thẳng a

a: \(a\perp\left(Q\right);\Delta\subset\left(Q\right)\)
=>\(\Delta\perp a\)(1)
\(b\perp\left(R\right);\Delta\subset\left(R\right)\)
=>\(\Delta\perp b\)(2)
mà a,b thuộc (P)(3)
nên từ (1), (2), (3) suy ra \(\Delta\perp\left(P\right)\)
b: Có 1 đường duy nhất

a) • Ta có: M ∈ b và (P) ∩ (Q) = b;
Suy ra M ∈ (P).
Mà M ∈ (M, a)
Do đó M là giao điểm của (P) và (M, a).
Lại có b’ = (P) ∩ (M, a)
Suy ra đường thẳng b’ đi qua M.
Tương tự ta cũng chứng minh được b’’ đi qua điểm M.
• Ta có: a // (P);
a ⊂ (M, a)
(M, a) ∩ (P) = b’
Do đó a // b’.
Tương tự ta cũng có a // b’’.
Do đó b’ // b’’.
Mặt khác: (P) ∩ (Q) = b;
(M, a) ∩ (P) = b’;
(M, a) ∩ (Q) = b’’;
b // b’’.
Do đó b // b’ // b’’.
Mà cả ba đường thẳng cùng đi qua điểm M nên ba đường thẳng này trùng nhau.
b) Vì a // b’ nên a // b (do b ≡ b’).
tham khảo
Ta có:\(a//\left(P\right)\)
\(a//\left(Q\right)\)
\(\left(P\right)\cap\left(Q\right)=b\)
Do đó theo hệ quả định lí \(2\) ta có \(a//b\).

Đường thẳng vuông góc với mặt phẳng được hiểu là đường thẳng nằm thẳng đứng so với mặt phẳng.

a:(P)//(Q)
a vuông góc (P)
=>a vuông góc (Q)
b: Chúng sẽ song song với nhau
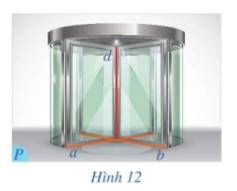
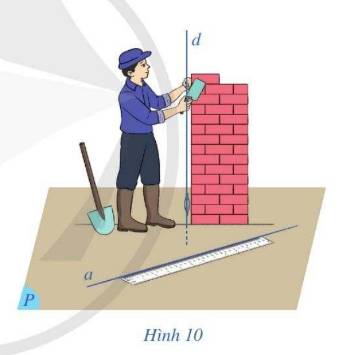
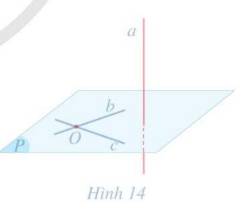

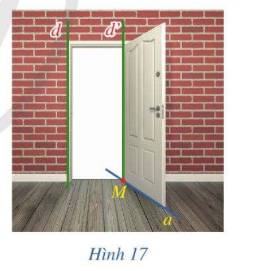


Đường thẳng d có vuông góc với mặt phẳng (P)
Vì: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b\end{array} \right. \Rightarrow d \bot \left( P \right)\)