
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\text{Δ}=\left(2m\right)^2-4m\left(m-2\right)=4m^2-4m^2+8m=8m\)
Để phương trình có hai nghiệm thì 8m>=0
hay m>=0
Theo đề, ta có: \(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=4\)
\(\Leftrightarrow\sqrt{\left(-2m\right)^2-4m\left(m-2\right)}=4\)
\(\Leftrightarrow\sqrt{8m}=4\)
=>m=2
\(\Delta'=m^2-m^2+2m=2m\)
Để pt có nghiệm khi m >= 0
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=m\left(m-2\right)\end{matrix}\right.\)
\(\left(x_1-x_2\right)^2\left(x_1+x_2\right)^2=16\Leftrightarrow\left[\left(x_1+x_2\right)^2-4x_1x_2\right]\left(x_1+x_2\right)^2=16\)
\(\Leftrightarrow\left[4m^2-4m\left(m-2\right)\right].4m^2=0\)
\(\Leftrightarrow8m.4m^2=0\Leftrightarrow m=0\)(tm)

a: \(A=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-1\right):\left(\dfrac{9-x}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-1\right):\dfrac{9-x+x-9-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{-\left(\sqrt{x}-2\right)^2}\)
\(=\dfrac{-3\left(\sqrt{x}-2\right)}{-\left(\sqrt{x}-2\right)^2}=\dfrac{3}{\sqrt{x}-2}\)

a: =>2x+1=27
=>2x=26
=>x=13
b: =>\(\sqrt[3]{x+5}=x+5\)
=>x+5=(x+5)^3
=>(x+5)(x+4)(x+6)=0
=>x=-5;x=-4;x=-6
c: =>2-3x=-8
=>3x=10
=>x=10/3
d: =>\(\sqrt[3]{x-1}=x-1\)
=>(x-1)^3=(x-1)
=>x(x-1)(x-2)=0
=>x=0;x=1;x=2

Giả sử tồn tại các số nguyên x,y thảo mãn \(x^4+y^3+4=0\) \(\left(1\right)\)
Ta có: \(\left(1\right)\) \(\Leftrightarrow\left(x^2-2x+2\right)\left(x^2+2x+2\right)=-y^3\)
Trước tiên ta nhận xét rằng x phải là một số lẻ, bởi ngược lại nếu x là một số chẵn thì \(x^4+4=-y^3\) là lập phương của một số chẵn, nhưng \(x^4+4\) không chia hết cho 8 với mọi số nguyên x ( vô lí ).
Vậy x là một số lẻ, suy ra y cũng là một số lẻ.
Đặt \(d=\left(x^2-2x+2,x^2+2x+2\right)\)
Ta có: \(4x=\left[\left(x^2+2x+2\right)-\left(x^2-2x+2\right)\right]⋮d\)
Mặt khác d là số lẻ ( vì \(-y^3⋮d\) và y là số lẻ ), dẫn đến \(\left(4,d\right)=1\) và do đó \(x⋮d\)
Suy ra \(2⋮d\) nên \(d=1\) ( vì d lẻ )
Tóm lại, hai số nguyên \(x^2-2x+2\) và \(x^2+2x+2\) là hai số nguyên tố cùng nhau, có tích là lập phương của một số nguyên nên mỗi số là lập phương của một số nguyên.
Đặt:
\(x^2-2x+2=a^3,x^2+2x+2=b^3\) với \(a,b\inℤ\)
Suy ra \(\left(x-1\right)^2=\left(a-1\right)\left(a^2+a+1\right)\)
\(\left(x+1\right)^2=b^3-1=\left(b-1\right)\left(b^2+b+1\right)\)
Do đó: \(a-1\ge0,b-1\ge0\)
Gọi \(d_1\) là ước chung lớn nhất của \(a-1\) và \(a^2+a=1\) thì \(3a=\left[\left(a^2+a+1\right)-\left(a-1\right)^2\right]⋮d_1\)
Mà \(\left(a,d_1\right)=1\) ( vì \(d_1\) là ước của \(a-1\) ) nên \(3⋮d_1\) )
Do đó: \(d_1\in\left\{1;3\right\}\)
Tương tự gọi \(d_2\) là ước chung lớn nhất của \(b-1\) và \(b^2+b+1\) thì \(d_2\in\left\{1;3\right\}\)
Chú ý rằng nếu \(d_1=d_2=3\) thì \(\left(x-1\right)^2\) và \(\left(x+1\right)^2\) đều chia hết cho 3
Suy ra \(2=\left(x+1\right)-\left(x-1\right)\) chia hết cho 3 ( vô lí )
Vì vậy trong hai số \(d_1,d_2\) phải có một số bằng 1
+ Nếu \(d_1=1\) thì khi đó \(a-1\) và \(a^2+a+1\) là hai số nguyên tố cùng nhau có tích là một số chính phương nên cả 2 số đó đồng thời là số chính phương.
Đặt \(a^2+a+1=m^2\) thì
\(4m^2=4\left(a^2+a=1\right)=\left(2a+1\right)^2+3\)
Do đó \(\left(2m-2a-1\right)\left(2m+2a+1\right)=3\)
TH1: \(2m-2a-1=1,2m+2a+1=3\) thì \(a=0\) ( vô lí vì phương trình \(x^2-2x+2\) không cs nghiệm nguyên )
TH2: \(2m-2a-1=3,2m+2a+1=1\) thì \(a=-1\) ( vô lí vì phương trình \(x^2-2x+2=-1\) không cs nghiệm nguyên )
+ Nếu \(d_2=1\) làm tương tự ta không tìm đc x,y thỏa mãn.
Vậy không tồn tại các số nguyên x,y thỏa mãn đề bài.

Gọi phương trình đường thẳng đi qua hai điểm A và B là: y = ax + by = ax+b. A thuộc đường thẳng y = ax + by = ax+b nên: 0.a + b = 2 ⇔ b = 2 0.a+b = 2⇔b = 2. B thuộc đường thẳng y = a x + b y=ax+b nên: ( − 3 ) a + b = 4 (−3)a+b=4 ⇔ a = 4 − b − 3 ⇔a=4−b−3 = 4 − 2 − 3 = − 2 3 =4−2−3=−23. Vậy phương trình đường thẳng AB là: y = − 2 3 x + 2 y=−23x+2. Do − 2 3 .6 + 2 = − 2 −23.6+2=−2 nên C thuộc đường thẳng AB hay A, B, C thẳng hàng.

Lời giải:

Lời giải:
$ABCD$ nội tiếp $(O)$ nên theo tính chất tgnt thì \(\widehat{MCB}=\widehat{MAD}\)
Xét tam giác $MCB$ và $MAD$ có:
\(\left\{\begin{matrix} \angle \text{M chung}\\ \widehat{MCB}=\widehat{MAD}\end{matrix}\right.\Rightarrow \triangle MCB\sim \triangle MAD(g.g)\)
\(\Rightarrow \frac{MC}{MB}=\frac{MA}{MD}\Leftrightarrow MC.MD=MA.MB(1)\)
Hoàn toàn tương tự: \(\triangle MC'B\sim \triangle MAD'\Rightarrow \frac{MC'}{MB}=\frac{MA}{MD'}\)
\(\Leftrightarrow MC'.MD'=MA.MB(2)\)
Từ \((1); (2)\Rightarrow MC.MD=MC'.MD'\Rightarrow \frac{MC}{MC'}=\frac{MD'}{MD}\)
Xét tam giác $MCC'$ và $MD'D$ có:
\(\left\{\begin{matrix} \angle \text{M chung}\\ \frac{MC}{MC'}=\frac{MD'}{MD}\end{matrix}\right.\) \(\Rightarrow \triangle MCC'\sim \triangle MD'D(c.g.c)\)
\(\Rightarrow \widehat{MCC'}=\widehat{MD'D}\Rightarrow CC'D'D\) nội tiếp.

a: CA vuông góc AB
=>CA là tiếp tuyến của (O)(Vì O là trung điểm của AB)
b: \(AB=\sqrt{3^2+4^2}=5\left(cm\right)\)
Xét ΔABC vuông tại A có AD là đường cao
nên AD^2=BD*DC
=>DC=3^2/4=2,25cm
BC=2,25+4=6,25cm
\(AC=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)



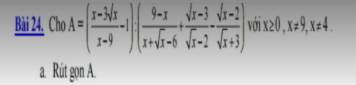 helpppp
helpppp
a: Xét tứ giác BNMC có
\(\widehat{BNC}=\widehat{BMC}=90^0\)
nên BNMC là tứ giác nội tiếp
Xét ΔABC có
BM,CN là các đường cao
BM cắt CN tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
b: Kẻ tiếp tuyến Ax của (O)
Xét (O) có
\(\widehat{xAC}\)là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{AMN}\left(=180^0-\widehat{NMC}\right)\)
nên \(\widehat{xAC}=\widehat{AMN}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ax//MN
Ta có: Ax//MN
AK\(\perp\)Ax
Do đó: AK\(\perp\)MN