Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vào đây nhé Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath

c: Trường hợp 1: n=2k
\(\Leftrightarrow n\left(n+2017\right)=2k\left(2k+2017\right)⋮2\)
Trường hợp 2: n=2k+1
\(\Leftrightarrow n\left(n+2017\right)=\left(2k+1\right)\left(2k+2018\right)⋮2\)

`<=> x(y - 2) + y - 2 + 3 = 0`
`<=> (x+1)(y-2) + 3 = 0`
`<=> (x+1)(y - 2) = -3`
`=> x + 1 in Ư(3)`
Đến đây chắc bạn tự làm được rồi ha, xét các ước của `x` và `y`.

theo bài ra ta thấy hình tam giác trên có 3 góc :BAC,ACB,ABC
có: góc ACB= 50 độ (1)
BAC= 90 độ(2)
ACB= 40 độ(3)
từ (1)(2)và (3) =>góc lớn nhất của tam giác ABC là góc BAC=90 độ
vậy...

TH1: với n<2018 ta có :
\(2^m+2017=-\left(n-2018\right)+\left(n-2018\right)=0\)
=> Không thể xảy ra vì \(2^m+2017>0\) Vì m là số tự nhiên
TH2 : với \(n\ge2018\)
=> \(2^m+2017=n-2018+n-2018=2\left(n-2018\right)\)
Ta có : Vế trái \(2^m+2017\) là số tựi nhiên lẻ => ko chia hết cho 2
Mà Vế phải 2(n-2018) luôn chia hết cho 2
=> Vô lí . Vậy pt vô nghiệm và m,n ko tồn tại

Đề dài quá. Bạn cần bài nào thì ghi chú rõ bài đó ra nhé. Nếu cần nhiều bài thì tách lẻ ra từng bài từng post để mọi người theo dõi và hỗ trợ nhanh hơn.

Ta có :
\(Q\left(x\right)=\left|x-2017\right|+\left|x-2018\right|+\left|x-2019\right|\)
\(Q\left(x\right)=\left|x-2018\right|+\left(\left|x-2017\right|+\left|x-2019\right|\right)\)
\(Q\left(x\right)=\left|x-2018\right|+\left(\left|x-2017\right|+\left|2019-x\right|\right)\)
Áp dụng bất đẳng thức giá trị tuyệt đối \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) dấu "=" xảy ra khi \(ab\ge0\) ta có :
\(\left|x-2017\right|+\left|2019-x\right|\ge\left|x-2017+2019-x\right|=\left|2\right|=2\)
Dấu "=" xảy ra khi \(\left(x-2017\right)\left(2019-x\right)\ge0\)
Trường hợp 1 :
\(\hept{\begin{cases}x-2017\ge0\\2019-x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge2017\\x\le2019\end{cases}}}\)
\(\Rightarrow\)\(2017\le x\le2019\)
Trường hợp 2 :
\(\hept{\begin{cases}x-2017\le0\\2019-x\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le2017\\x\ge2019\end{cases}}}\) ( loại )
Suy ra : \(Q\left(x\right)=\left|x-2018\right|+2\ge2\)
Dấu "=" xảy ra khi \(\left|x-2018\right|=0\)
\(\Leftrightarrow\)\(x-2018=0\)
\(\Leftrightarrow\)\(x=2018\) ( thoã mãn \(2017\le x\le2019\) )
Vậy giá trị nhỏi nhất của \(Q\left(x\right)=2\) khi \(x=2018\)
Chúc bạn học tốt ~
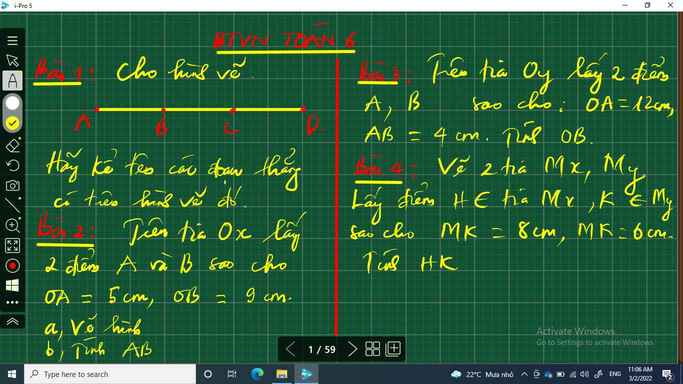
 help me, pls. Sắp đến giờ nộp bài rồi, các bn giúp mình với
help me, pls. Sắp đến giờ nộp bài rồi, các bn giúp mình với

không cíu đc :>
=> lỗi :>
thanh niên vui tính