K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 9 2021
\(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|4\overrightarrow{MB}-\overrightarrow{MC}\right|\)
⇔ \(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|3\overrightarrow{MB}+\overrightarrow{CB}\right|\) (1)
Trên cạnh AB lấy O sao cho \(\dfrac{OA}{OB}=\dfrac{1}{2}\)
⇒ \(2\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{0}\)
Trên cạnh tia đối của tia BC lấy E sao cho \(\dfrac{EB}{BC}=\dfrac{1}{3}\)
⇒ \(3\overrightarrow{EB}+\overrightarrow{CB}=\overrightarrow{0}\)
Vậy (1) ⇒ \(\left|3\overrightarrow{MO}+2\overrightarrow{OA}+\overrightarrow{OB}\right|=\left|3\overrightarrow{ME}+3\overrightarrow{EB}+\overrightarrow{CB}\right|\)
⇒ 3MO = 3ME
⇒ MO = ME
⇒ M nằm trên đường trung trực của OE
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
d. G thuộc Ox nên \(G\left(2;0\right)\)
d qua G nên:
\(2\left(m^2-3m\right)+2m-5=0\)
\(\Leftrightarrow2m^2-4m-5=0\Rightarrow m=\dfrac{2\pm\sqrt{14}}{2}\)
b.
H thuộc Oy nên: \(H\left(0;3\right)\)
d qua H nên:
\(0\left(m^2-3m\right)+2m-5=3\)
\(\Rightarrow2m=8\Rightarrow m=4\)
18 tháng 10 2021
Bài 2:
ĐKXĐ: \(\left\{{}\begin{matrix}-3< x< 3\\x\ge2\end{matrix}\right.\Leftrightarrow2\le x< 3\)
4 tháng 3 2018
Đặt:
\(L=\sqrt{a+2009}+\sqrt{b+2009}+\sqrt{c+2009}\)
\(L^2=\left(\sqrt{a+2009}+\sqrt{b+2009}+\sqrt{c+2009}\right)^2\)
\(\le\left(1^2+1^2+1^2\right)\left(a+b+c+6027\right)\) (bđt bunhiacopxki)
\(=3\left(2+6027\right)=18087\Leftrightarrow A\le\sqrt{18087}\)
p/s: đề đã fix vì t thấy số qá to:v
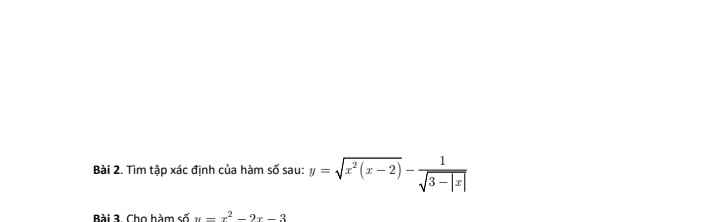
ta co 2x<=x^2+1 cosi
\(\sqrt{2x-1}\le\sqrt{x^2+1-1}=\sqrt{x^2}\)=|x|
..............................