PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
2 tháng 4 2017
Thể tích của hình cần tính gồm:
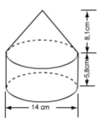
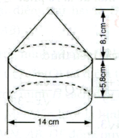
Một hình trụ đường kính đáy 14cm chiều cao 5,8cm (V1):
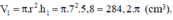
Một hình nón đường kính đáy 14cm chiều cao 8,1cm (V2)
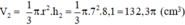
Thể tích hình cần tính:
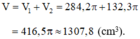
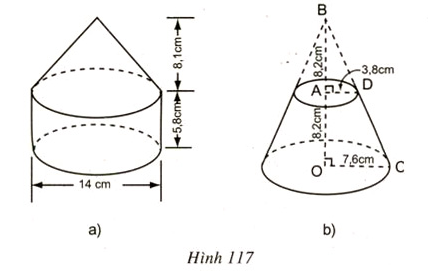
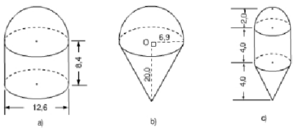
b) Thể tích cần tính là một hình nón cụt, chiều cao 8,2cm; bán kính đường tròn của đáy trên và đáy dưới theo thứ tự là 3,8cm và 7,6cm. Cách tính là lấy thể tích hình nón lớn trừ đi thể tích hình nón bé.
PT
1
CM
13 tháng 11 2017
Thể tích của hình cần tính gồm:
Một hình trụ đường kính đáy 14cm chiều cao 5,8cm (V1):
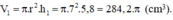
Một hình nón đường kính đáy 14cm chiều cao 8,1cm (V2)
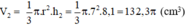
Thể tích hình cần tính:
SG
2
17 tháng 4 2017
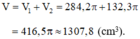
Hướng dẫn trả lời:
- Hình a:
Thể tích hình trụ có đường kính đáy 14cm, đường cao 5,8cm
V1 = π . r2h = π. 72. 5,8 = 284,2 π (cm3)
Thể tích hình nón có đường kính đáy 14cm và đường cao 8,1 cm.
V2=13πr2h=13π.72.8,1=132,3π(cm3)V2=13πr2h=13π.72.8,1=132,3π(cm3)
Vậy thể tích hình cần tính là:
V = V1 + V2 = 2,84,2π + 132,3π = 416,5π (cm3)
- Hình b)
Thể tích hình nón lớn: V1=13πr2h1=13π(7,6)2.16,4=991,47(cm3)V1=13πr2h1=13π(7,6)2.16,4=991,47(cm3)
Thể tích hình nón nhỏ: V2=13πr2h2=13π(3,8)2.8,2=123,93(cm3)V2=13πr2h2=13π(3,8)2.8,2=123,93(cm3)
Thể tích hình nón cần tính là: V = V1 – V2 = 991,47 – 123,93 = 867,54 cm3
PT
1
PT
1
CM
10 tháng 9 2018
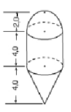
Thể tích của hình cần tính gòm thể tích của một hình nón cộng với thể tích của nửa hình cầu.
PT
1
CM
29 tháng 4 2017
Thể tích của hình cần tính gồm thể tích của một hình trụ cộng với thể tích của một nửa hình cầu.
Thể tích hình trụ:
Thể tích nửa hình cầu:
Thể tích của hình:
V = V 1 + V 2
≈ 1570 , 31 c m 3
PT
1
CM
7 tháng 2 2019
a, Gọi thể tích của hình trụ và hình nón lần lượt V 1 ; V 2 . Hình trụ và hình nón cùng có bán kính bằng r = 7cm
Ta có thể tích của hình cần tìm là: với h 1 ; h 2 lần lượt là chiều cao ứng với hình trụ và hình nón
Thay số ta được V = 416 , 5 πcm 3
b, Thể tích hình nón cụt là: V n c = 1 3 πh r 1 2 + r 1 r 2 + r 2 2
Thay số vào và tính toán ta được V n c = 276 , 3 πcm 3
Thể tích hình nón là: V n = 1 3 πr 2 h
Thay số ta được V n = 315 , 8 πcm 3
SG
1
17 tháng 4 2017
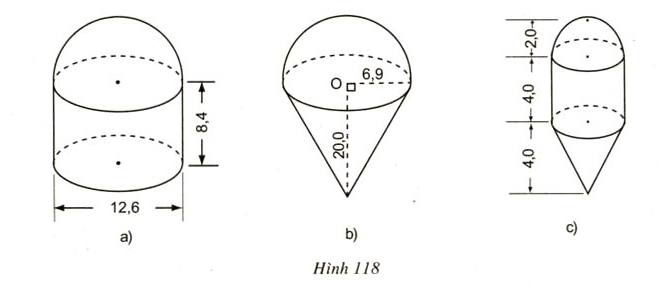
Hướng dẫn trả lời:
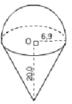
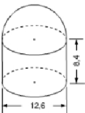
Hình a.
V=π(12,62)2.8,4+12.43π(12,62)3=13π(6,9)2.(8,4+12,63)=500,094π(cm3)V=π(12,62)2.8,4+12.43π(12,62)3=13π(6,9)2.(8,4+12,63)=500,094π(cm3)
Vậy Vhình a = 500,094π cm3
Hình b.
V=13π(6,9)2.20+12.43π.(6,9)3=13π(6,9)2(20+13,8)=536,406π(cm3)V=13π(6,9)2.20+12.43π.(6,9)3=13π(6,9)2(20+13,8)=536,406π(cm3)
Vậy Vhình b = 536, 406π cm3
Hình c.
V=13π.22.4+π.22.4+12.43π.23=4.22.π(13+1+13)=80π3(cm3)V=13π.22.4+π.22.4+12.43π.23=4.22.π(13+1+13)=80π3(cm3)
Vậy Vhình c =
b
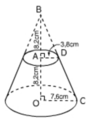
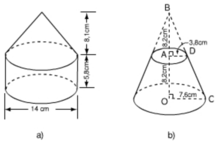
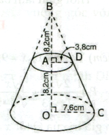
Thể tích cần tính là một hình nón cụt, chiều cao 8,2cm; bán kính đường tròn của đáy trên và đáy dưới theo thứ tự là 3,8cm và 7,6cm. Cách tính là lấy thể tích hình nón lớn trừ đi thể tích hình nón bé.
Thể tích hình nón là:
Thể tích hình nón nhỏ:
Thể tích cần tính là:
V = V l ớ n - V n h ỏ